Question

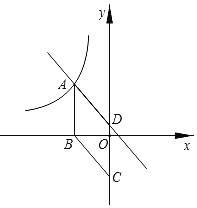
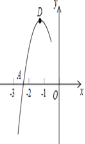
【题目】抛物线y=ax2+bx+c的顶点为D（﹣1，2），与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图所示，则以下结论：①b2﹣4ac＜0；②a+b+c＜0；③c﹣a =2；④方程ax2+bx+c=0有两个相等的实数根．其中正确结论的个数为（　　）

A.1个B.2个C.3个D.4个

Answer 1

【答案】B

【解析】

先从二次函数图像获取信息，运用二次函数的性质一—判断即可．

解：∵二次函数与x轴有两个交点，∴b2-4ac>0，故①错误；

∵抛物线与x轴的另一个交点为在（0，0）和（1，0）之间，且抛物线开口向下，

∴当x=1时,有y=a+b+c＜0，故②正确;

∵函数图像的顶点为（-1，2）

∴a-b+c=2，

又∵由函数的对称轴为x=-1，

∴=-1,即b=2a

∴a-b+c =a-2a+c=c-a=2，故③正确；

由①得b2-4ac>0，则ax2+bx+c =0有两个不等的实数根，故④错误；

综上，正确的有两个．

故选：B．