题目内容

如图，点A在反比例函数 $数学公式$ 的图象上，过A作AB⊥x轴与反比例函数 $数学公式$ 的图象交于点B，点C为y轴上任意一点，则△ABC的面积为________．

$\text{[math]}$
分析：连结OA、OB，AB与x轴交于D点，由于AB⊥x轴，根据同底等高的三角形面积相等得S_△ABC=S_△OAB，再根据反比例函数y= $\text{[math]}$ （k≠0）比例系数数k的几何意义得到S_△OAD= $\text{[math]}$ ×|3|= $\text{[math]}$ ，S_△OBD= $\text{[math]}$ ×|-6|=3，然后求它们的和即可得到答案．
解答：连结OA、OB，AB与x轴交于D点，如图

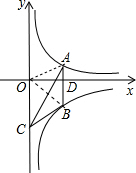
∵AB⊥x轴，
∴S_△ABC=S_△OAB，
∵S_△OAD= $\text{[math]}$ ×|3|= $\text{[math]}$ ，S_△OBD= $\text{[math]}$ ×|-6|=3，
∴S_△OAB= $\text{[math]}$ +3= $\text{[math]}$ ．
∴S_△ABC= $\text{[math]}$ ．
故答案为 $\text{[math]}$ ．
点评：本题考查了反比例函数y= $\text{[math]}$ （k≠0）比例系数数k的几何意义：过反比例函数图象上任意一点分别作x轴、y轴的垂线，则垂线与坐标轴所围成的矩形的面积为|k|．

练习册系列答案

精典练习系列答案

经纶学典精讲精练系列答案

聚焦小考冲刺48天系列答案

聚焦新中考系列答案

鸿翔教育决胜中考系列答案

绝对名师系列答案

开心教程系列答案

开心15天精彩寒假巧计划江苏凤凰科学技术出版社系列答案

考出好成绩系列答案

考能大提升系列答案

相关题目

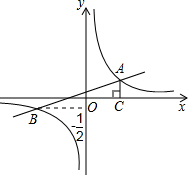如图，已知在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=

（m≠0）的图象相交于A、B两点，且点B的纵坐标为-

，过点A作AC⊥x轴于点C，AC=1，OC=2．
求：（1）求反比例函数和一次函数的关系式；
（2）直接写出反比例函数值大于一次函数值时x的取值范围．

如图1，点D在反比例函y=

(k＞0)的图象上，△ODC是以CO为斜边的等腰直角三角形，且C （4，0）．
（1）求k的值；
（2）将线段DC平移至线段D₁C₁，D₁在x轴的负半轴上，C₁在双曲线y=

上，求点D₁的坐标；
（3）如图2，双曲线y=

的图象上有两个动点A（a，m），B（3a，b），（a＞0），求S_△OAB的值．

如图1，点D在反比例函 $数学公式$ 的图象上，△ODC是以CO为斜边的等腰直角三角形，且C （4，0）．
（1）求k的值；
（2）将线段DC平移至线段D₁C₁，D₁在x轴的负半轴上，C₁在双曲线 $数学公式$ 上，求点D₁的坐标；
（3）如图2，双曲线 $数学公式$ 的图象上有两个动点A（a，m），B（3a，b），（a＞0），求S_△OAB的值．

如图，已知在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数

（m≠0）的图象相交于A、B两点，且点B的纵坐标为

，过点A作AC⊥x轴于点C，AC=1，OC=2．
求：（1）求反比例函数和一次函数的关系式；
（2）直接写出反比例函数值大于一次函数值时x的取值范围．

如图，Rt△AOB中，O为坐标原点，∠AOB=90°，OA∶OB＝1∶2，如果点A在反比例函

数y=(x>0)的图像上运动，那么点B在函数 (填函数解析式)的图像上运动．