题目内容
 如图在△ABC中,∠A=60°,∠B:∠ACB=1:5,则∠ACD=________.
如图在△ABC中,∠A=60°,∠B:∠ACB=1:5,则∠ACD=________.
80°
分析:根据三角形内角和等于180°求出∠B+∠ACB,然后求出∠B,再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解.
解答:∵∠A=60°,
∴∠B+∠ACB=180°-60°=120°,
∵∠B:∠ACB=1:5,
∴∠B=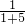 ×120°=20°,
×120°=20°,
∴∠ACD=∠A+∠B=60°+20°=80°.
故答案为:80°.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形内角和定理,熟记性质是解题的关键.
分析:根据三角形内角和等于180°求出∠B+∠ACB,然后求出∠B,再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解.
解答:∵∠A=60°,
∴∠B+∠ACB=180°-60°=120°,
∵∠B:∠ACB=1:5,
∴∠B=
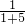 ×120°=20°,
×120°=20°,∴∠ACD=∠A+∠B=60°+20°=80°.
故答案为:80°.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形内角和定理,熟记性质是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

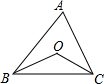 如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为
如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为 如图在△ABC中,∠A=45°,tanB=3,BC=
如图在△ABC中,∠A=45°,tanB=3,BC= 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE, 如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是
如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是