题目内容
(10分)如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个动点到达终点时,另一个动点也随之停止运动.

(1)求AC、BC的长;
(2)设点P的运动时间为x(秒),△PBQ的面积为y(cm2),当△PBQ存在时,求y与x的函数关系式,并写出自变量x的取值范围;
(3)当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为定点的三角形与△ABC是否相似,请说明理由;
(4)当x=5秒时,在直线PQ上是否存在一点M,使△BCM得周长最小,若存在,求出最小周长,若不存在,请说明理由。
(1)AC=8cm BC=6cm (2)y= (3)见解析 (4)16
(3)见解析 (4)16
【解析】
试题分析:(1)设AC=4x,BC=3x,根据勾股定理进行求解;(2)分两种情况来进行讨论,分别求出函数解析式;(3)利用三角形相似的条件来进行计算;(4)利用轴对称的性质来进行计算.

试题解析:(1)设AC=4x,BC=3x,在Rt△ABC中,AC²+BC²=AB²,即:(4x)²+(3x)²=10²,
解得:x=2,∴AC=8cm,BC=6cm;
(2)①、∵△QHB∽△ACB, ∴ ,
,
∴QH= x,y=
x,y= BP·QH=
BP·QH= (10-x)·
(10-x)· x=-
x=- x²+8x(0<x≤3),
x²+8x(0<x≤3),
②当点Q在边CA上运动时,过点Q作QH′⊥AB于H′,∵AP=x,∴BP=10-x,AQ=14-2x,∵△AQH′∽△ABC, ∴ ,即:
,即: ,解得:QH′=
,解得:QH′= (14-x),
(14-x),
∴y= PB·QH′=
PB·QH′= (10-x)·
(10-x)· (14-x)=
(14-x)= x²-
x²- x+42(3<x<7);
x+42(3<x<7);
∴y与x的函数关系式为:y= ;
;

(3)∵AP=x,AQ=14-x, ∵PQ⊥AB,∴△APQ∽△ACB,∴ ,
,
即: ,解得:x=
,解得:x= ,PQ=
,PQ= ,∴PB=10-x=
,∴PB=10-x= ,∴
,∴ ,
,
∴当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为定点的三角形与△ABC不相似;
(4)存在,理由:∵AQ=14-2x=14-10=4,AP=x=5,∵AC=8,AB=10,∴PQ是△ABC的中位线,
∴PQ∥AB,∴PQ⊥AC, ∴PQ是AC的垂直平分线,∴PC=AP=5,∴当点M与P重合时,△BCM的周长最小, ∴△BCM的周长为:MB+BC+MC=PB+BC+PC=5+6+5=16,
∴△BCM的周长最小值为16。


考点:三角形相似的应用、勾股定理、二次函数的实际应用

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 D.3
D.3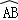 的长等于( )
的长等于( ) B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
 +kx+b经过点P(2,-3),Q(-1,0).
+kx+b经过点P(2,-3),Q(-1,0).
 ,与
,与 轴交点为
轴交点为 .求
.求 的值.
的值. 轴的另一个交点为
轴的另一个交点为 ,求四边形
,求四边形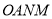 的面积.
的面积. ,点A的坐标为(0,1),则点E的坐标是 .
,点A的坐标为(0,1),则点E的坐标是 .
 = .
= .