题目内容
【题目】在现实生活中,我们会看到许多“标准”的矩形,如我们的课本封面、A4的打印纸等,其实这些矩形的长与宽之比都为 ![]() :1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.
:1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.
(1)如图①,求证:BA=BP;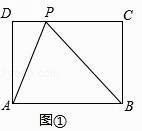
(2)如图②,点Q在DC上,且DQ=CP,若G为BC边上一动点,当△AGQ的周长最小时,求 ![]() 的值;
的值;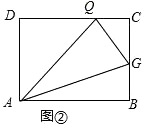
(3)如图③,已知AD=1,在(2)的条件下,连接AG并延长交DC的延长线于点F,连接BF,T为BF的中点,M、N分别为线段PF与AB上的动点,且始终保持PM=BN,请证明:△MNT的面积S为定值,并求出这个定值.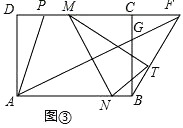
【答案】
(1)
证明:如图①中,设AD=BC=a,则AB=CD= ![]() a.
a.

∵四边形ABCD是矩形,
∴∠C=90°,
∵PC=AD=BC=a,
∴PB= ![]() =
= ![]() a,
a,
∴BA=BP
(2)
解:如图②中,作Q关于BC的对称点Q′,连接AQ′交BC于G,此时△AQG的周长最小.
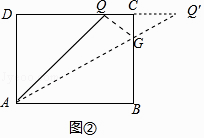
设AD=BC=QD=a,则AB=CD= ![]() a,
a,
∴CQ=CQ′= ![]() a﹣a,
a﹣a,
∵CQ′//AB,
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
(3)
证明:如图③中,作TH//AB交NM于H,交BC于K.
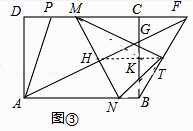
由(2)可知,AD=BC=1,AB=CD= ![]() ,DP=CF=
,DP=CF= ![]() ﹣1,
﹣1,
∵S△MNT= ![]() THCK+
THCK+ ![]() THBK=
THBK= ![]() HT(KC+KB)=
HT(KC+KB)= ![]() HTBC=
HTBC= ![]() HT,
HT,
∵TH//AB//FM,TF=TB,
∴HM=HN,
∴HT= ![]() (FM+BN),
(FM+BN),
∵BN=PM,
∴HT= ![]() (FM+PM)=
(FM+PM)= ![]() PF=
PF= ![]() (1+
(1+ ![]() ﹣1)=
﹣1)= ![]() ,
,
∴S△MNT= ![]() HT=
HT= ![]() =定值
=定值
【解析】(1)如图①中,设AD=BC=a,则AB=CD= ![]() a.通过计算得出AB=BP=
a.通过计算得出AB=BP= ![]() a,由此即可证明;(2)如图②中,作Q关于BC的对称点Q′,连接AQ′交BC于G,此时△AQG的周长最小.设AD=BC=QD=a,则AB=CD=
a,由此即可证明;(2)如图②中,作Q关于BC的对称点Q′,连接AQ′交BC于G,此时△AQG的周长最小.设AD=BC=QD=a,则AB=CD= ![]() a,可得CQ=CQ′=
a,可得CQ=CQ′= ![]() a﹣a,由CQ′//AB,推出
a﹣a,由CQ′//AB,推出 ![]() =
= ![]() =
= ![]() =
= ![]() ;(3)如图③中,作TH//AB交NM于H,交BC于K.由S△MNT=
;(3)如图③中,作TH//AB交NM于H,交BC于K.由S△MNT= ![]() THCK+
THCK+ ![]() THBK=
THBK= ![]() HT(KC+KB)=
HT(KC+KB)= ![]() HTBC=
HTBC= ![]() HT,利用梯形的中位线定理求出HT即可解决问题;
HT,利用梯形的中位线定理求出HT即可解决问题;

 名校课堂系列答案
名校课堂系列答案【题目】北京地铁1号线是中国最早的地铁线路,2000年实现了23个车站的贯通运营,该线西起苹果园站,东至四惠东站,全长约31千米.下表是北京地铁1号线首末车时刻表,开往四惠东方向和苹果园方向的首车的平均速度均为每小时60千米,求由苹果园站和四惠东站开出的首车第一次相遇的时间.
北京地铁1号线首末车时刻表 | ||||
车站名称 | 往四惠东方向 | 往苹果园方向 | ||
首车时间 | 末车时间 | 首车时间 | 末车时间 | |
苹果园 | 5:10 | 22:55 | -- | -- |
… | … | … | … | … |
四惠东 | -- | -- | 5:05 | 23:15 |