��Ŀ����
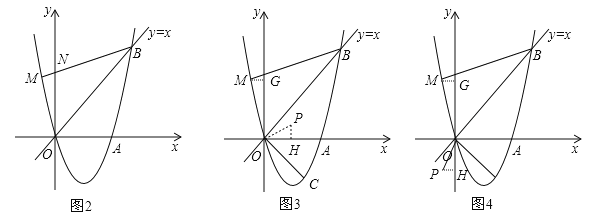
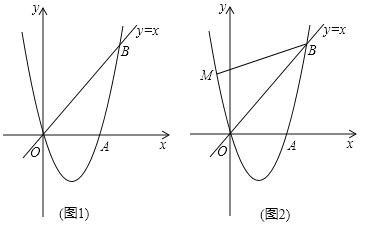
����Ŀ����ͼ1������ԭ��O��������![]() ��a��0����x�ύ����һ��A��
��a��0����x�ύ����һ��A��![]() ��0�����ڵ�һ��������ֱ��y=x���ڵ�B��2��t����
��0�����ڵ�һ��������ֱ��y=x���ڵ�B��2��t����
��1�������������ߵı���ʽ��
��2���ڵ��������ڵ�����������һ��C��������B��O��CΪ����������ε����Ϊ2�����C�����ꣻ
��3����ͼ2������M�������������ϣ�����MBO=��ABO���ڣ�2���������£��Ƿ���ڵ�P��ʹ����POC�ס�MOB�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��C��1����1������3��������P������Ϊ��
����2��C��1����1������3��������P��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��������
�����������1����ֱ�߽���ʽ�����B�����꣬��A��B���꣬���ô���ϵ��������������ߵı���ʽ��
��2����C��CD��y�ᣬ��x���ڵ�E����OB�ڵ�D����B��BF��CD�ڵ�F�������C�����꣬����C������ɱ�ʾ��CD�ij����Ӷ��ɱ�ʾ����BOC��������������ɵõ�����C������ķ��̣������C�����ꣻ
��3����MB��y���ڵ�N�����֤����ABO�ա�NBO�������N�����꣬�����ֱ��BN�Ľ���ʽ������ֱ��BM�������߽���ʽ�����M�����꣬��M��MG��y���ڵ�G����B��C����������OB��OC�ij��������������ε����ʿ����![]() ��ֵ������P�ڵ�һ������ʱ����P��PH��x���ڵ�H����������֤����MOG�ס�POH����
��ֵ������P�ڵ�һ������ʱ����P��PH��x���ڵ�H����������֤����MOG�ס�POH����![]() =
=![]() =
=![]() ��ֵ�������PH��OH�������P�����ꣻ��P���ڵ�������ʱ��ͬ�������P�����꣮
��ֵ�������PH��OH�������P�����ꣻ��P���ڵ�������ʱ��ͬ�������P�����꣮
���������
��1����B��2��t����ֱ��y=x�ϣ���t=2����B��2��2������A��B����������������߽���ʽ�ɵ���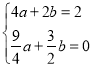 �������
�������![]() ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2����ͼ1����C��CD��y�ᣬ��x���ڵ�E����OB�ڵ�D����B��BF��CD�ڵ�F������C���������ϵ������ĵ㣬������C��t��2t2��3t������E��t��0����D��t��t������OE=t��BF=2��t��CD=t����2t2��3t��=��2t2+4t����S��OBC=S��CDO+S��CDB=![]() CDOE+
CDOE+![]() CDBF=
CDBF=![]() ����2t2+4t����t+2��t��=��2t2+4t���ߡ�OBC�����Ϊ2������2t2+4t=2�����t1=t2=1����C��1����1����
����2t2+4t����t+2��t��=��2t2+4t���ߡ�OBC�����Ϊ2������2t2+4t=2�����t1=t2=1����C��1����1����
��3�����ڣ���MB��y���ڵ�N����ͼ2����B��2��2�������AOB=��NOB=45�㣬����AOB����NOB�����ߡ�AOB=��NOB��OB=OB����ABO=��NBO�����AOB�ա�NOB��ASA������ON=OA=![]() ����N��0��
����N��0��![]() ����������ֱ��BN����ʽΪy=kx+
����������ֱ��BN����ʽΪy=kx+![]() ����B���������ɵ�22k+
����B���������ɵ�22k+![]() �����k=
�����k=![]() ����ֱ��BN�Ľ���ʽΪ
����ֱ��BN�Ľ���ʽΪ![]() ������ֱ��BN�������߽���ʽ�ɵ���
������ֱ��BN�������߽���ʽ�ɵ���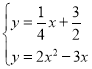 �������
�������![]() ��
��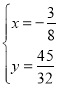 ����M��
����M��![]() ��
��![]() ������C��1����1�������COA=��AOB=45�㣬��B��2��2������OB=
������C��1����1�������COA=��AOB=45�㣬��B��2��2������OB=![]() ��OC=
��OC=![]() ���ߡ�POC�ס�MOB����
���ߡ�POC�ס�MOB����![]() =
=![]() =2����POC=��BOM������P�ڵ�һ����ʱ����ͼ3����M��MG��y���ڵ�G����P��PH��x���ڵ�H����ͼ3
=2����POC=��BOM������P�ڵ�һ����ʱ����ͼ3����M��MG��y���ڵ�G����P��PH��x���ڵ�H����ͼ3
�ߡ�COA=��BOG=45�㣬���MOG=��POH������PHO=��MGO�����MOG�ס�POH����![]() =
=![]() =
=![]() =2����M��
=2����M��![]() ��
��![]() ������MG=
������MG=![]() ��OG=
��OG=![]() ����PH=
����PH=![]() MG=
MG=![]() ��OH=
��OH=![]() OG=
OG=![]() ����P��
����P��![]() ��
��![]() ����
����
����P�ڵ�������ʱ����ͼ4����M��MG��y���ڵ�G����P��PH��y���ڵ�H��ͬ�������PH=![]() MG=
MG=![]() ��OH=
��OH=![]() OG=
OG=![]() ����P����
����P����![]() ��
��![]() ����
����
���Ͽ�֪���������������ĵ�P��������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ����
����