题目内容
5.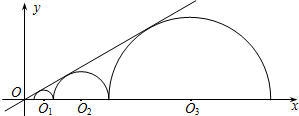 如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线$y=\frac{{\sqrt{3}}}{3}x$相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当r1=1时,r2015=32014.
如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线$y=\frac{{\sqrt{3}}}{3}x$相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当r1=1时,r2015=32014.
分析 过C1、C2、C3、…、Cn作直线y=$\frac{\sqrt{3}}{3}$x的垂线,垂足分别为A1、A2、A3、An,如图,根据切线的性质得C1A1⊥OA1,C2A2⊥OA2,C3A3⊥OA,…,CnAn⊥OAn,再确定直线y=$\frac{\sqrt{3}}{3}$x与x轴的正半轴的夹角为30°,接着利用两圆相切的性质得到C1C2=r1+r2,C2C3=r2+r3,…,然后根据含30度的直角三角形三边的关系,在Rt△OC1A1中得到OC1=2C1A1=2,在Rt△OC2A2中得到2+1+r2=2r2,解得r2=3=31,在Rt△OC3A3中得到6+3+r3=2r3,解得r3=9=32,再观察计算出来的半径得到半径都是3的正整数指数幂,且指数比序号数小1,于是得rn=3n-1.
解答 解:过C1、C2、C3、…、Cn作直线y=$\frac{\sqrt{3}}{3}$x的垂线,垂足分别为A1、A2、A3、An,如图,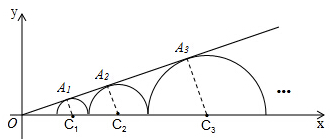
∵a个半圆弧都与直线y=$\frac{\sqrt{3}}{3}$x相切,
∴C1A1⊥OA1,C2A2⊥OA2,C3A3⊥OA,…,CnAn⊥OAn,
∵x=1时,y=$\frac{\sqrt{3}}{3}$x=$\frac{\sqrt{3}}{3}$,
∴直线y=$\frac{\sqrt{3}}{3}$x与x轴的正半轴的夹角为30°,
∵a个半圆弧依次相外切,
∴C1C2=r1+r2,C2C3=r2+r3,…,
在Rt△OC1A1中,OC1=2C1A1=2,
在Rt△OC2A2中,OC2=2C2A2,则2+1+r2=2r2,解得r2=3=31,
在Rt△OC3A3中,OC3=2C3A3,则6+3+r3=2r3,解得r3=9=32,
在Rt△OC4A4中,OC4=2C4A4,则18+9+r4=2r4,解得r4=27=33,
由此可得rn=3n-1.
∴r2015=32014,
故答案为:32014.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了一次函数图象上点的坐标特征.

| A. | 2 | B. | 3 | C. | 4 | D. | -8 |
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
| A. | 4a4 | B. | -4a4 | C. | -4a3 | D. | 4a3 |
 如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.
如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.