题目内容
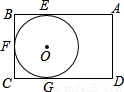
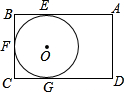 定义:定点与⊙O上任意一点之间距离的最小值称为点与⊙O之间的距离.现有一矩形ABCD如图所示,AB=14,BC=12,⊙O与矩形的边AB、BC、CD分别相切于点E、F、G,则点A与⊙O之间的距离为
定义:定点与⊙O上任意一点之间距离的最小值称为点与⊙O之间的距离.现有一矩形ABCD如图所示,AB=14,BC=12,⊙O与矩形的边AB、BC、CD分别相切于点E、F、G,则点A与⊙O之间的距离为分析:连接OA,交⊙O于H,则AH即为所求的距离;连接OE、OF,易证得四边形OEBF是正方形,即可求得⊙O的半径及AE的长,进而可由勾股定理求得OA的长,则AH=OA-R,由此得解.
解答: 解:连接OE、OF,则OE⊥AB,OF⊥BC;
解:连接OE、OF,则OE⊥AB,OF⊥BC;
又∠B=90°,且OE=OF,∴四边形OEBF是正方形;
∴OE=OF=BF=BE=
BC=6;
∴AE=AB-BE=8;
连接OA,交⊙O于H;
Rt△AOE中,OE=6,AE=8;由勾股定理得:OA=10,
∴AH=OA-OH=10-6=4;
即点A与⊙O之间的距离为4.
 解:连接OE、OF,则OE⊥AB,OF⊥BC;
解:连接OE、OF,则OE⊥AB,OF⊥BC;又∠B=90°,且OE=OF,∴四边形OEBF是正方形;
∴OE=OF=BF=BE=
| 1 |
| 2 |
∴AE=AB-BE=8;
连接OA,交⊙O于H;
Rt△AOE中,OE=6,AE=8;由勾股定理得:OA=10,
∴AH=OA-OH=10-6=4;
即点A与⊙O之间的距离为4.
点评:此题主要考查了矩形的性质、切线的性质、勾股定理的应用等知识;能够发现四边形OEBF是正方形,并正确地得到OE、BE的长,是解答此题的关键.

练习册系列答案
相关题目
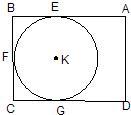 10、定义:定点A与⊙O上任意一点之间的距离的最小值称为点A与⊙O之间的距离.现有一矩形ABCD(如图),AB=14cm,BC=12cm,⊙K与矩形的边AB,BC,CD分别切于点E,F,G,则点A与⊙K的距离为( )
10、定义:定点A与⊙O上任意一点之间的距离的最小值称为点A与⊙O之间的距离.现有一矩形ABCD(如图),AB=14cm,BC=12cm,⊙K与矩形的边AB,BC,CD分别切于点E,F,G,则点A与⊙K的距离为( )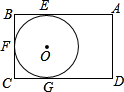 定义:定点与⊙O上任意一点之间距离的最小值称为点与⊙O之间的距离.现有一矩形ABCD如图所示,AB=14,BC=12,⊙O与矩形的边AB、BC、CD分别相切于点E、F、G,则点A与⊙O之间的距离为________.
定义:定点与⊙O上任意一点之间距离的最小值称为点与⊙O之间的距离.现有一矩形ABCD如图所示,AB=14,BC=12,⊙O与矩形的边AB、BC、CD分别相切于点E、F、G,则点A与⊙O之间的距离为________.