题目内容
【题目】在四边形![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上运动.
上运动.
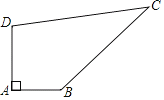
(1)如图1,已知![]() .
.

①若![]() 平分
平分![]() ,则
,则![]() ______;
______;
②若![]() ,试说明
,试说明![]() ;
;
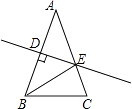
(2)如图2,已知![]() ,试说明
,试说明![]() 平分
平分![]() .
.

【答案】(1)①90°;②证明见解析;(2)证明见解析.
【解析】
(1)①由![]() 可得
可得![]() ,根据平行线的性质可得∠ABC+∠BCD=180°,已知BF平分∠ABC,CE平分∠BCD,由角平分线的定义可得∠FBC=
,根据平行线的性质可得∠ABC+∠BCD=180°,已知BF平分∠ABC,CE平分∠BCD,由角平分线的定义可得∠FBC=![]() ∠ABC,∠BCF=
∠ABC,∠BCF=![]() ∠BCD,所以∠FBC+∠BCF=
∠BCD,所以∠FBC+∠BCF=![]() ∠ABC+
∠ABC+![]() ∠BCD=
∠BCD=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×180°=90°,即可得∠BFC=90°;②已知CE平分∠BCD,由角平分线的定义可得∠DCE=∠BCF,根据等角的余角相等可得∠FBC=∠DEC;再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得
×180°=90°,即可得∠BFC=90°;②已知CE平分∠BCD,由角平分线的定义可得∠DCE=∠BCF,根据等角的余角相等可得∠FBC=∠DEC;再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得![]() ;(2)已知CE平分∠BCD,由角平分线的性质可得∠DCE=∠BCF,由三角形的内角和定理可证得∠FBC=∠DEC;由∠BFC+∠BFE=180°,∠BFC=∠A,可得∠BFE+∠A=180°,再由四边形的内角和为360°可得∠ABF+∠AEF=180°,再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得
;(2)已知CE平分∠BCD,由角平分线的性质可得∠DCE=∠BCF,由三角形的内角和定理可证得∠FBC=∠DEC;由∠BFC+∠BFE=180°,∠BFC=∠A,可得∠BFE+∠A=180°,再由四边形的内角和为360°可得∠ABF+∠AEF=180°,再利用同角的补角相等证得∠ABF=∠DEC,所以∠DEC=∠ABF=∠FBC,即可得![]() .
.
(1)∵![]() ,
,
∴![]() ,
,
∴∠ABC+∠BCD=180°,
∵BF平分∠ABC,CE平分∠BCD,
∴∠FBC=![]() ∠ABC,∠BCF=
∠ABC,∠BCF=![]() ∠BCD,
∠BCD,
∴∠FBC+∠BCF=![]() ∠ABC+
∠ABC+![]() ∠BCD=
∠BCD=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×180°=90°,
×180°=90°,
∴∠BFC=90°;
故答案为:90°;
②∵CE平分∠BCD,
∴∠DCE=∠BCF,
∵∠BFC=∠D=90°,
∴∠BCF+∠FBC=90°,∠DEC+∠ECD=90°,
∴∠FBC=∠DEC;
∵∠ABF+∠AEF=180°,∠DEC+∠AEF=180°,
∴∠ABF=∠DEC,
∴∠DEC=∠ABF=∠FBC,
∴![]() ;
;
(2)∵CE平分∠BCD,
∴∠DCE=∠BCF,
∵∠BFC=∠D,
∴∠FBC=∠DEC;
∵∠BFC+∠BFE=180°,∠BFC=∠A,
∴∠BFE+∠A=180°,
∴∠ABF+∠AEF=180°,
∵∠DEC+∠AEF=180°,
∴∠ABF=∠DEC,
∴∠DEC=∠ABF=∠FBC,
∴![]() .
.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案