��Ŀ����
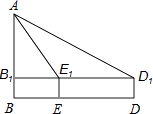
����Ŀ����ͼ1���ڡ�ABC�У���AB=c��BC=a��AC=b������AE��BF�ཻ��G����AE��BF��
��1���ٵ���ABF=60�㣬c=4ʱ����a��b��ֵ��
�ڵ���ABF=30�㣬c=2 ![]() ʱ��a= �� b=��
ʱ��a= �� b=��
��2���ɣ�1�������ʾ������a2 �� b2 �� c2����֮������������ϵʽ������ֱ��д�������
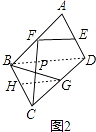
��3����ͼ2����ƽ���ı���ABCD�У�AB=4 ![]() ��BC=3
��BC=3 ![]() ����E��F��G�ֱ���AD��AB��CD���е㣬CF��BG����P�㣬��EF��FC�����ã�2���еĽ��ۣ���BG�ij���
����E��F��G�ֱ���AD��AB��CD���е㣬CF��BG����P�㣬��EF��FC�����ã�2���еĽ��ۣ���BG�ij���
���𰸡�
��1��![]() ��
��![]()
��2��a2+b2=5c2
��3��
�⣺ȡBC���е�H������HG��DB����ͼ2��
��E��F��G�ֱ���AD��AB��CD���е㣬
��EF��DB��HG��
��BF��CG��BF=CG��
���BFP=��GCP��
�ڡ�BFP���PCG�У� 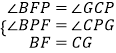 ��
��
���BFP�ա�PCG��
��PF=CP��
��P��BG���е㣬
�֡�EF��FC��
��HG��PC��
�ɣ�2����֪BC2+BG2=5CG2��
��AB=4 ![]() ��BC=3
��BC=3 ![]() ��
��
�ࣨ3 ![]() ��2+BG2=5��2
��2+BG2=5��2 ![]() ��2��
��2��
��BG= ![]() ��
��
���������⣺��1���١�AE��BF����ABF=60�㣬AB=4��
����Rt��ABG��BG= ![]() AB=2��AG=ABcos60��=2
AB=2��AG=ABcos60��=2 ![]() ��
��
��AE��BF�ǡ�ABC�����ߣ�
��FG= ![]() BG=1a2+b2=5c2
BG=1a2+b2=5c2
��Rt��AGF��AF= ![]() =
= ![]() ��
��
��AC=b=2 ![]() ��
��
ͬ���ɵ�BC=a=2 ![]() ��
��
�ڵ���ABF=30�㣬AB=2 ![]() ��
��
����Rt��ABG��AG= ![]() AB=
AB= ![]() ��BG=ABcos30��=3��
��BG=ABcos30��=3��
��FG= ![]() BG=
BG= ![]() ��
��
��Rt��AGF��AF= ![]() =
= ![]() ��
��
��AC=b= ![]() ��
��
ͬ����BC=a= ![]() ��
��
���Դ��ǣ� ![]() ��
�� ![]() ����2�����룺a2+b2=5c2 ��
����2�����룺a2+b2=5c2 ��
�ɢٿ�֪��a2=28��b2=52��c2=16��
��a2+b2=52+28=80=5��16=5c2 ��
��a2+b2=5c2 ��
�ɢڿ�֪��a2=39��b2=21��c2=12��
��a2+b2=39+21=60=5��12=5c2 ��
��a2+b2=5c2 ��
���Դ���a2+b2=5c2��
�����㾫����ͨ���������ƽ���ı��ε����ʣ�����ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�ּ����Խ����⣮