题目内容
如图是一个常见文件铁夹的侧面示意图,OA,OB表示铁夹的两个面,且OA=OB,C是轴心,即C到OA,OB的距离相等.CD⊥OA于点D,DA=15mm,DC=10mm,∠AOB=45°.我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的 距离,参考数据:sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41.
距离,参考数据:sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41.
解:连接OC并延长交AB于E,
因为夹子是轴对称图形,故OE是对称轴,
∴OE⊥AB,AE=BE,
∵∠COD=∠AOE,∠CDO=∠AEO=90°,
∴Rt△OCD∽Rt△OAE,
∴ ,
,
∵OA=OB,∠AOB=45°.
∴∠COD=22.5°,
∴sin22.5°=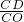 =0.38mm,
=0.38mm,
∴OC= ≈26mm,
≈26mm,
∴OD= =24mm,
=24mm,
∴ ,
,
∴AE=15mm,
∴AB=2AE=30mm.
分析:根据轴对称的性质求出Rt△OCD∽Rt△OAE,再根据相似三角形的对应边成比例及勾股定理求出AB的长即可.
点评:此题是相似三角形在实际生活中的运用,解答此题的关键是根据题意画出图形,由相似三角形的性质解答.
因为夹子是轴对称图形,故OE是对称轴,

∴OE⊥AB,AE=BE,
∵∠COD=∠AOE,∠CDO=∠AEO=90°,
∴Rt△OCD∽Rt△OAE,
∴
 ,
,∵OA=OB,∠AOB=45°.
∴∠COD=22.5°,
∴sin22.5°=
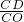 =0.38mm,
=0.38mm,∴OC=
 ≈26mm,
≈26mm,∴OD=
 =24mm,
=24mm,∴
 ,
,∴AE=15mm,
∴AB=2AE=30mm.
分析:根据轴对称的性质求出Rt△OCD∽Rt△OAE,再根据相似三角形的对应边成比例及勾股定理求出AB的长即可.
点评:此题是相似三角形在实际生活中的运用,解答此题的关键是根据题意画出图形,由相似三角形的性质解答.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 距离,参考数据:sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41.
距离,参考数据:sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41.