题目内容
说明连续五个自然数的和为什么一定能被5整除.
分析:设五个连续自然数中的第一个为a,则这五个连续的自然数可表示为a、a+1,a+2,a+2,a+4.其和为:a+(a+1)+(a+2)+(a+3)+(a+4)=5×(a+2),依此即可作出判断.
解答:解:设五个连续自然数中的第一个为a,则这五个连续的自然数可表示为a、a+1,a+2,a+2,a+4.
其和为:a+(a+1)+(a+2)+(a+3)+(a+4)
=a+a+1+a+2+a+3+a+4
=5a+10
=5×(a+2).
所以连续五个自然数的和为什么一定能被5整除.
其和为:a+(a+1)+(a+2)+(a+3)+(a+4)
=a+a+1+a+2+a+3+a+4
=5a+10
=5×(a+2).
所以连续五个自然数的和为什么一定能被5整除.
点评:考查了整式的加减,本题是根据相邻的两个自然数相差1的特点从而求出五个连续自然数的和是5的倍数的.

练习册系列答案
相关题目
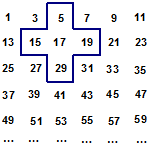 将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.
将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.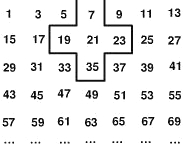
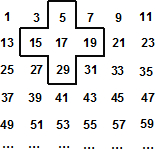 将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数.
将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数. 将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数.
将连续的奇数1,3,5,7,…,排成如下图的数表,用图中所示的十字框可任意框出5个数. 将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.
将连续的奇数1,3,5,7,…,排成如图所示的数表,用十字框任意框出5个数.