题目内容
【题目】已知:![]() 为
为![]() 的直径,
的直径,![]() ,
,![]() 为
为![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合).
重合).

(1)如图1,若![]() 平分
平分![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .①求证:
.①求证:![]() ;②若
;②若![]() ,求
,求![]() 的长;
的长;
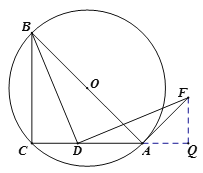
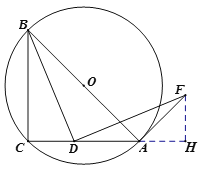
(2)如图2,若![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() .求证:
.求证:![]() 为
为![]() 的切线.
的切线.
【答案】(1)①见解析,②2;(2)见解析
【解析】
(1)①先根据圆周角定理得出![]() ,再得出
,再得出![]() ,再根据角平分线的定义得出
,再根据角平分线的定义得出![]() ,最后根据三角形外角定理即可求证;②取
,最后根据三角形外角定理即可求证;②取![]() 中点
中点![]() ,连接
,连接![]() ,可得
,可得![]() 是中位线,根据平行线的性质得
是中位线,根据平行线的性质得![]() ,然后根据等腰三角形的性质得出
,然后根据等腰三角形的性质得出![]() ,最后再根据中位线的性质得出
,最后再根据中位线的性质得出![]() ;
;
(2)![]() 上截取
上截取![]() ,连接
,连接![]() ,由题意先得出
,由题意先得出![]() ,再得出
,再得出![]() ,然后由旋转性质得
,然后由旋转性质得![]() 、
、![]() ,再根据同角的补角相等得出
,再根据同角的补角相等得出![]() ,然后证的
,然后证的![]() ,最后得出
,最后得出![]() 即可证明.
即可证明.
解:(1)①证明:![]() 为
为![]() 的直径,
的直径,
![]() .
.
![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() 平分
平分![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ;
;
②解法一:如图,取![]() 中点
中点![]() ,连接
,连接![]() ,
,
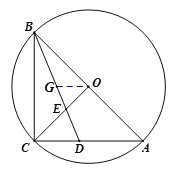
![]() 为
为![]() 的中点,
的中点,
![]() ,
,![]() .
.
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() ;
;
解法二:如图,作![]() ,垂足为
,垂足为![]() ,
,
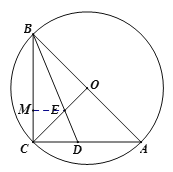
![]() 平分
平分![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
在![]() 中,
中,![]() .
.
![]() ;
;
解法三:如图,作![]() ,垂足为
,垂足为![]() ,
,
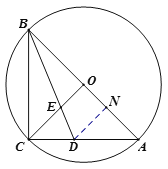
设![]()
![]() 平分
平分![]() ,
,![]() ,
,
![]() .
.
![]()
∴![]()
∴![]() ,即
,即![]()
∴![]()
解得:![]()
∴![]()
(2)证明(法一):如图,在![]() 上截取
上截取![]() ,连接
,连接![]() .
.
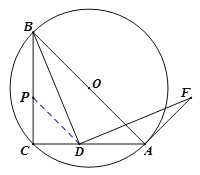
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
由旋转性质得,![]() ,
,![]() .
.
![]()
![]() ,
,
![]() .
.
![]() .(
.(![]() 没写不扣分)
没写不扣分)
![]() .
.
![]() .
.
![]() .
.
![]() 为
为![]() 的切线.
的切线.
证法二:如图,延长![]() 到
到![]() ,使
,使![]() .
.
由旋转性质得,![]() ,
,![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() .(
.(![]() 没写不扣分)
没写不扣分)
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() 为
为![]() 的切线.
的切线.
证法三:作![]() 交
交![]() 延长线于点
延长线于点![]() .(余下略)
.(余下略)
由旋转性质得,![]() ,
,![]()
∴![]()
![]() ,
,
∴![]() .
.
∵![]()
∴![]()
∴![]() 、
、![]()
![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵![]() 为
为![]() 的直径,
的直径,
∴![]()
∴![]()
∴![]()
∴![]() .
.
∴![]() 为
为![]() 的切线.
的切线.

练习册系列答案
相关题目