题目内容
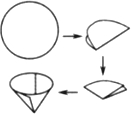 化学实验课上,小明用一张圆形滤纸做一个过滤器:先将圆形滤纸对折成半圆形,再对折成四分之一圆形,然后打开得到圆锥形过滤器.若已知圆形滤纸的直径为10cm,则滤纸重叠部分每层面积
化学实验课上,小明用一张圆形滤纸做一个过滤器:先将圆形滤纸对折成半圆形,再对折成四分之一圆形,然后打开得到圆锥形过滤器.若已知圆形滤纸的直径为10cm,则滤纸重叠部分每层面积分析:此题是圆锥侧面积求解的典型问题,要灵活运用公式,并结合实际解题.
解答:解:如果抽象地将母线长为6cm,开口圆直径为7.2cm的特殊规格的漏斗内壁圆锥侧面展开,得到的扇形弧长为7.2πcm,
圆心角为7.2π÷6×
=216°,
滤纸片如紧贴漏斗壁,其围成圆锥的最外层侧面展开图的圆心角也应为216°,
又∵重叠部分每层面积为圆形滤纸片的面积减去围成圆锥的最外层侧面展开图的面积的差的一半,
∴滤纸重叠部分每层面积=(25π-
×25π)÷2=5π(cm2).
故答案为:5π.
圆心角为7.2π÷6×
| 180° |
| π |
滤纸片如紧贴漏斗壁,其围成圆锥的最外层侧面展开图的圆心角也应为216°,
又∵重叠部分每层面积为圆形滤纸片的面积减去围成圆锥的最外层侧面展开图的面积的差的一半,
∴滤纸重叠部分每层面积=(25π-
| 216 |
| 360 |
故答案为:5π.
点评:本题考查了圆锥的计算,将几何图形做适当变形,找出隐藏条件是解一些复杂几何问题常用的方法.

练习册系列答案
相关题目
 化学实验课上,小明用一张圆形滤纸做一个过滤器:先将圆形滤纸对折成半圆形,再对折成四分之一圆形,然后打开得到圆锥形过滤器.若已知圆形滤纸的直径为10cm,则这个过滤器的高是________cm.
化学实验课上,小明用一张圆形滤纸做一个过滤器:先将圆形滤纸对折成半圆形,再对折成四分之一圆形,然后打开得到圆锥形过滤器.若已知圆形滤纸的直径为10cm,则这个过滤器的高是________cm.