题目内容

已知△ABC中，D、E分别为AB、AC上的点，且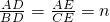 $数学公式$ ，CD交BE于O，连AO并延长交BC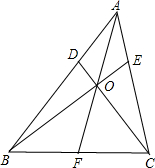于F．
（1）当 $数学公式$ 时，求 $数学公式$ 的值；
（2）当n=1时，求证：BF=CF；
（3）当n=______时，O为AF中点．

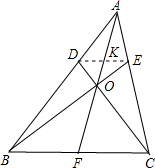解：（1）连接DE交AF于K，
∵ $\text{[math]}$ ，
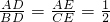∴DE∥BC，
∴ $\text{[math]}$ ， $\text{[math]}$ ，
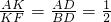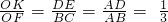∴设OK=a，则OF=3a，
∴KF=4a，
∴AK=2a，
∴OA=AK+OK=3a，
∴ $\text{[math]}$ =1；

（2）∵n=1时，AD=BD，AE=CE，
∴O是△ABC的重心，
∴AF是△ABC的中线，
∴BF=CF；

（3）∵ $\text{[math]}$ ，
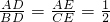∴DE∥BC，
∴ $\text{[math]}$ ， $\text{[math]}$ ，
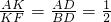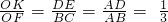∴设OK=a，则OF=3a，
∴KF=4a，
∴AK=2a，
∴OA=AK+OK=3a，
∴ $\text{[math]}$ =1，
∴当n= $\text{[math]}$ 时，O为AF中点．
故答案为： $\text{[math]}$ ．
分析：（1）连接DE交AF于K，根据平行线分线段成比例定理，即可证得DE∥BC，继而可得 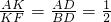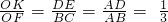$\text{[math]}$ ， $\text{[math]}$ ，根据比例的性质，即可求得 $\text{[math]}$ 的值；
（2）由n=1时，AD=BD，AE=CE，可得O是△ABC的重心，继而可得BF=CF；
（3）根据（1）的证明方法，即可求得答案．
点评：此题考查了平行线分线段成比例定理与比例的性质．此题难度适中，解题的关键是数形结合思想的应用与辅助线的作法．