题目内容
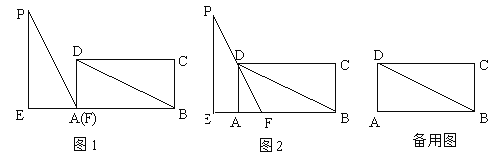
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠,顶点
折叠,顶点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处,延长
处,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
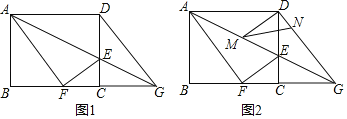
(1)求线段![]() 的长;
的长;
(2)如图2,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的动点(与端点不重合),且
上的动点(与端点不重合),且![]() ,设
,设![]() ,
,![]() .
.
①写出![]() 关于
关于![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的最小值;
的最小值;
②是否存在这样的点![]() ,使
,使![]() 是等腰三角形?若存在,请求出
是等腰三角形?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)①当
;(2)①当![]() 时,
时,![]() 有最小值,最小值
有最小值,最小值![]() ;②存在.满足条件的
;②存在.满足条件的![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
![]() 由翻折可知:
由翻折可知:![]() ,设
,设![]() ,则
,则![]() 在
在![]() 中,利用勾股定理构建方程即可解决问题.
中,利用勾股定理构建方程即可解决问题.![]() 证明
证明![]() ∽
∽![]() ,可得
,可得![]() ,由此即可解决问题.
,由此即可解决问题.![]() 有两种情形:如图
有两种情形:如图![]() 中,当
中,当![]() 时
时![]() 如图
如图![]() 中,当
中,当![]() 时,作
时,作![]() 于
于![]() 分别求解即可解决问题.
分别求解即可解决问题.
解:(1)如图1中,
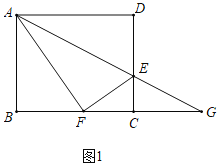
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
由翻折可知:![]() .
.![]() ,设
,设![]() ,则
,则![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
在![]() 中,则有:
中,则有:![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)①如图2中,
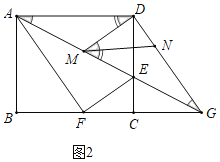
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
当![]() 时,
时,![]() 有最小值,最小值
有最小值,最小值![]() .
.
②存在.有两种情形:如图3-1中,当![]() 时,
时,
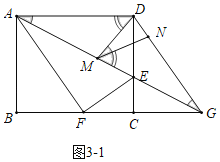
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
如图3-2中,当![]() 时,作
时,作![]() 于
于![]() .
.
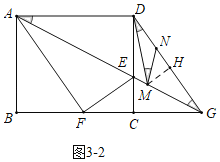
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
综上所述,满足条件的![]() 的值为
的值为![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目