题目内容
(2004•济南)已知抛物线y=- x2+(6-
x2+(6-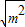 )x+m-3与x轴有A、B两个交点,且A、B两点关于y轴对称.
)x+m-3与x轴有A、B两个交点,且A、B两点关于y轴对称.(1)求m的值;
(2)写出抛物线解析式及顶点坐标;
(3)根据二次函数与一元二次方程的关系,将此题的条件换一种说法写出来.
【答案】分析:(1)根据与x轴的两个交点的横坐标即是一元二次方程的两个根,再根据两个点关于y轴对称,则横坐标和为0,即方程的两根之和是0,求得m的值;
(2)根据(1)的结论即可解答;
(3)由(1)的分析,即方程- x2+(6-
x2+(6-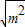 )x+m-3=O的两根互为相反数.
)x+m-3=O的两根互为相反数.
解答:解:(1)设A(x1,0)B(x2,0).
∵A、B两点关于y轴对称,
∴6-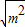 =0,
=0,
∴m=±6.
当m=-6时,此方程无实数根,应舍去.
∴m=6;
(2)求得y=- x2+3.顶点坐标是(0,3);
x2+3.顶点坐标是(0,3);
(3)方程- x2+(6-
x2+(6-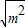 )x+m-3=0的两根互为相反数(或两根之和为零等).
)x+m-3=0的两根互为相反数(或两根之和为零等).
点评:此题考查了二次函数和一元二次方程之间的联系.特别注意根据根与系数的关系求得的字母的值,一定要代入原方程检验,看方程是否有根.
(2)根据(1)的结论即可解答;
(3)由(1)的分析,即方程-
 x2+(6-
x2+(6-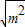 )x+m-3=O的两根互为相反数.
)x+m-3=O的两根互为相反数.解答:解:(1)设A(x1,0)B(x2,0).
∵A、B两点关于y轴对称,
∴6-
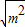 =0,
=0,∴m=±6.
当m=-6时,此方程无实数根,应舍去.
∴m=6;
(2)求得y=-
 x2+3.顶点坐标是(0,3);
x2+3.顶点坐标是(0,3);(3)方程-
 x2+(6-
x2+(6-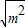 )x+m-3=0的两根互为相反数(或两根之和为零等).
)x+m-3=0的两根互为相反数(或两根之和为零等).点评:此题考查了二次函数和一元二次方程之间的联系.特别注意根据根与系数的关系求得的字母的值,一定要代入原方程检验,看方程是否有根.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
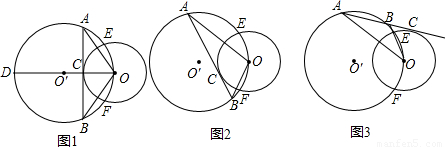

 =0,计算
=0,计算 •
• 的值.
的值. =0,计算
=0,计算 •
• 的值.
的值.