题目内容
解方程:
(1)2x2+3x-1=0;
(2)(x+4)2=5(x+4)
解:(1)∵a=2,b=3,c=-1,
∴b2-4ac=32-4×2×(-1)=17,
∴x= ,
,
∴x1=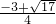 ,x2=
,x2= ;
;
(2)∵(x+4)2-5(x+4)=0,
∴(x+4)(x+4-5)=0,
∴x+4=0或x+4-5=0,
∴x1=-4,x2=1.
分析:(1)先计算出b2-4ac=32-4×2×(-1)=17,然后利用一元二次方程的求根公式解方程;
(2)先移项得到(x+4)2-5(x+4)=0,然后利用提公因式法把方程左边因式分解得到(x+4)(x+4-5)=0,于是一元二次方程转化为两个一元一次方程x+4=0或x+4-5=0,然后解一元一次方程即可.
点评:本题考查了解一元二次方程-因式分解法:先把方程化为一般式ax2+bx+c=0(a≠0),再把方程左边因式分解,然后把一元二次方程转化为两个一元一次方程,再解一元一次方程得到一元二次方程的解.也考查了利用公式法解一元二次方程.
∴b2-4ac=32-4×2×(-1)=17,
∴x=
 ,
,∴x1=
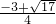 ,x2=
,x2= ;
;(2)∵(x+4)2-5(x+4)=0,
∴(x+4)(x+4-5)=0,
∴x+4=0或x+4-5=0,
∴x1=-4,x2=1.
分析:(1)先计算出b2-4ac=32-4×2×(-1)=17,然后利用一元二次方程的求根公式解方程;
(2)先移项得到(x+4)2-5(x+4)=0,然后利用提公因式法把方程左边因式分解得到(x+4)(x+4-5)=0,于是一元二次方程转化为两个一元一次方程x+4=0或x+4-5=0,然后解一元一次方程即可.
点评:本题考查了解一元二次方程-因式分解法:先把方程化为一般式ax2+bx+c=0(a≠0),再把方程左边因式分解,然后把一元二次方程转化为两个一元一次方程,再解一元一次方程得到一元二次方程的解.也考查了利用公式法解一元二次方程.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目