题目内容
如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足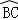 =
=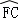 ,过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点.
,过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点.
(1)求证:AE⊥DE;
(2)若tan∠CBA=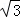 ,AE=3,求AF的长.
,AE=3,求AF的长.
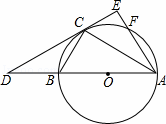
(1)证明:连接OC,
∵OC=OA,
∴∠BAC=∠OCA,
∵ =
= ,
,
∴∠BAC=∠EAC,
∴∠EAC=∠OCA,
∴OC∥AE,
∵DE且⊙O于点C,
∴OC⊥DE,
∴AE⊥DE;
(2)解:∵AB是⊙O的直径,
∴△ABC是直角三角形,
∵tan∠CBA= ,
,
∴∠CBA=60°,
∴∠BAC=∠EAC=30°,
∵△AEC为直角三角形,AE=3,
∴AC=2 ,
,
连接OF,
∵OF=OA,∠OAF=∠BAC+∠EAC=60°,
∴△OAF为等边三角形,
∴AF=OA= AB,
AB,
在Rt△ACB中,AC=2 ,tan∠CBA=
,tan∠CBA= ,
,
∴BC=2,
∴AB=4,
∴AF=2.


练习册系列答案
相关题目
因式分解a2b﹣b的正确结果是( )
|
| A. | b(a+1)(a﹣1) | B. | a(b+1)(b﹣1) | C. | b(a2﹣1) | D. | b(a﹣1)2 |
已知一组数据:1,2,6,3,3,下列说法正确的是( )
|
| A. | 众数是3 | B. | 中位数是6 | C. | 平均数是4 | D. | 方差是5 |
如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是( )

|
| A. |
| B. |
| C. |
| D. |
|
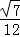 B.
B. 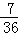
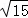 C.
C. 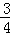
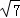 D.
D. 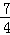
 第1次对折后得到的图形面积为S1,第2次对折后得到的图形面积为S2,…,第n次对折后得到的图形面积为Sn,请根据图2化简,S1+S2+S3+…+S2014=
第1次对折后得到的图形面积为S1,第2次对折后得到的图形面积为S2,…,第n次对折后得到的图形面积为Sn,请根据图2化简,S1+S2+S3+…+S2014=





 +1=
+1= .
.