题目内容
 已知:如图,AD∥OB,OC平分∠AOB,P是OC上一点,过点P作直线MN,分别交AD、OB于点M和N,且MP=NP.
已知:如图,AD∥OB,OC平分∠AOB,P是OC上一点,过点P作直线MN,分别交AD、OB于点M和N,且MP=NP.求证:点P到AO和AD的距离相等.
分析:过点P作PE⊥OB于点E,PF⊥OA于点F,PG⊥AD于点G,根据角平分线上的点到角的两边的距离相等可得PE=PF,根据两直线平行,内错角相等可得∠PNE=∠PMG,然后利用“角角边”证明△PEN和△PGM全等,根据全等三角形对应边相等可得PE=PG,从而得到PF=PG.
解答: 证明:如图,过点P作PE⊥OB于点E,PF⊥OA于点F,PG⊥AD于点G,
证明:如图,过点P作PE⊥OB于点E,PF⊥OA于点F,PG⊥AD于点G,
∵OC平分∠AOB,PE⊥OB于点E,PF⊥OA于点F,
∴PE=PF,
∵AD∥OB,
∴∠PNE=∠PMG,
在△PEN和△PGM中,
,
∴△PEN≌△PGM(AAS),
∴PE=PG,
∴PF=PG,
即点P到AO和AD的距离相等.
 证明:如图,过点P作PE⊥OB于点E,PF⊥OA于点F,PG⊥AD于点G,
证明:如图,过点P作PE⊥OB于点E,PF⊥OA于点F,PG⊥AD于点G,∵OC平分∠AOB,PE⊥OB于点E,PF⊥OA于点F,
∴PE=PF,
∵AD∥OB,
∴∠PNE=∠PMG,
在△PEN和△PGM中,
|
∴△PEN≌△PGM(AAS),
∴PE=PG,
∴PF=PG,
即点P到AO和AD的距离相等.
点评:本题考查了全等三角形的判定与性质,角平分线上的点到角的两边的距离相等的性质,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 27、已知:如图,AD∥BC,ED∥BF,且AF=CE.
27、已知:如图,AD∥BC,ED∥BF,且AF=CE. 25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.
25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.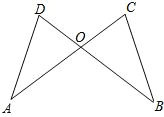 已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由.
已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由.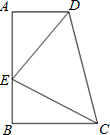 已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC.
已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC. 根据题意填空:
根据题意填空: