Question

23、小明为测量池塘的宽度，在池塘的两侧A，B分别引两条直线AC，BC，相交于点C，在BC上分别取点E，G，使BE=CG，再分别过点E，G作EF∥AB，GH∥AB，交AC于点F，H，测出EF=10m，GH=4m（如图）．小明就得出了结论：池塘的宽AB为14m．你认为小明的结论正确吗？请说明你的理由．

Answer 1

分析：过点E作ED∥AC，交AB于点D．只要证明四边形ADEF是平行四边形且△BDE≌△GHC即可．

解答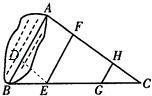：解：正确．
理由：过点E作ED∥AC，交AB于点D，
∵EF∥AB，
∴四边形ADEF是平行四边形，
∴AD=EF，ED∥AC，
∴∠BED=∠C，∠BDE=∠A，
∵GH∥AB，
∴∠A=∠CHG
∴∠CHG=∠BDE
∴△BDE≌△GHC，
∴BD=HG
∴AB=AD+BD=EF+HG=14．

点评：本题让我们了解测量两点之间的距离不止一种，只要符合平行四边形及全等三角形全等的条件，方案的操作性强，需要测量的线段和角度在陆地一侧即可实施．