题目内容
如图,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.对于本题小丽是这样证明的,请你将她的证明过程补充完整.证明:∵∠BAP与∠APD互补,(已知)
∴AB∥CD.( )
∴∠BAP=∠APC.( )
∵∠BAE=∠CPF,(已知)
∴∠BAP-∠BAE=∠APC-∠CPF,
( )
即 = .( )
∴AE∥FP.
∴∠E=∠F.

【答案】分析:已知∠BAP与∠APD互补,根据同旁内角互补两直线平行,可得AB∥CD,再根据平行线的判定与性质及等式相等的性质即可得出答案.
解答:证明:∵∠BAP与∠APD互补,根据同旁内角互补两直线平行,∴AB∥CD.
由两直线平行,内错角相等,∴∠BAP=∠APC,
∵∠BAE=∠CPF,(已知)
由等式的性质得:∴∠BAP-∠BAE=∠APC-∠CPF,
再根据等角减去等角得等角:即∠EAP=∠APE,
∴AE∥FP.
∴∠E=∠F.
点评:本题考查了平行线的判定与性质,属于基础题,关键是正确理解与运用平行线的判定与性质.
解答:证明:∵∠BAP与∠APD互补,根据同旁内角互补两直线平行,∴AB∥CD.
由两直线平行,内错角相等,∴∠BAP=∠APC,
∵∠BAE=∠CPF,(已知)
由等式的性质得:∴∠BAP-∠BAE=∠APC-∠CPF,
再根据等角减去等角得等角:即∠EAP=∠APE,
∴AE∥FP.
∴∠E=∠F.
点评:本题考查了平行线的判定与性质,属于基础题,关键是正确理解与运用平行线的判定与性质.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
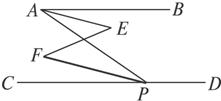 4、如图,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.对于本题小丽是这样证明的,请你将她的证明过程补充完整.
4、如图,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.对于本题小丽是这样证明的,请你将她的证明过程补充完整. 如图,∠BAP+∠APD=180°,∠1=∠2,那么AE与FP平行吗?请说明理由.
如图,∠BAP+∠APD=180°,∠1=∠2,那么AE与FP平行吗?请说明理由. 如图,∠BAP+∠APD=180°,∠1=∠2,那么AE与FP平行吗?请说明理由.
如图,∠BAP+∠APD=180°,∠1=∠2,那么AE与FP平行吗?请说明理由. 证明:∵∠BAP与∠APD互补,(已知)
证明:∵∠BAP与∠APD互补,(已知)