题目内容
已知抛物线y=-| 2 |
| 3 |
| 8 |
| 3 |
(1)若ABCD为正方形,求它的边长.
(2)是否存在周长为9的这样的矩形?试述理由.
分析:(1)根据题意,若设A点坐标为(x,0)则B为(4-x,0),D为(x,-
x2+
),再由ABCD为正方形,其边相等,即可求出x的值,继而求出边长.
(2)求出矩形ABCD的最大周长,发现9>其最大周长,故不存在这样的矩形.
| 2 |
| 3 |
| 8 |
| 3 |
(2)求出矩形ABCD的最大周长,发现9>其最大周长,故不存在这样的矩形.
解答: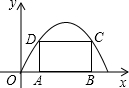 解:设A(x,0),则B(4-x,0),D(x,-
解:设A(x,0),则B(4-x,0),D(x,-
x2+
).(2分)
(1)若ABCD为正方形,则
4-2x=-
x2+
x(2分)
解得x=1或x=6(舍去)
∴正方形的边长为2.(2分)
(2)矩形周长y=(-
x2+
x+4-2x)×2
=-
x2+
x+8.(2分)
则x=
时,y有最大值=8
,
故周长为9的矩形不存在.(2分)
 解:设A(x,0),则B(4-x,0),D(x,-
解:设A(x,0),则B(4-x,0),D(x,-| 2 |
| 3 |
| 8 |
| 3 |
(1)若ABCD为正方形,则
4-2x=-
| 2 |
| 3 |
| 8 |
| 3 |
解得x=1或x=6(舍去)
∴正方形的边长为2.(2分)
(2)矩形周长y=(-
| 2 |
| 3 |
| 8 |
| 3 |
=-
| 4 |
| 3 |
| 4 |
| 3 |
则x=
| 1 |
| 2 |
| 1 |
| 3 |
故周长为9的矩形不存在.(2分)
点评:本题考查了二次函数的知识,难度适中,注意数形结合根据题意画出图形解题,同时要注意总结这类综合题的解题思路.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2011•金东区模拟)已知抛物线
(2011•金东区模拟)已知抛物线 B中点,点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上,且EO=ED.
B中点,点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上,且EO=ED.