题目内容
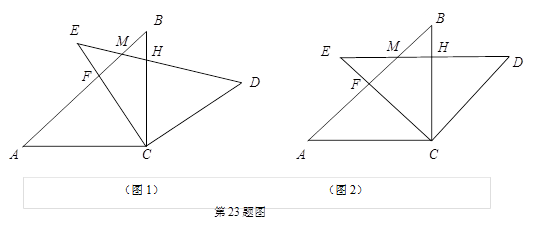
(本题满分12分,每小题满分各6分)如图(1),在△ABC和△EDC中,A C=CE=CB=CD,∠ACB=∠ECD=
C=CE=CB=CD,∠ACB=∠ECD= ,AB与CE交于F,ED与AB、BC分别交于M、H.
,AB与CE交于F,ED与AB、BC分别交于M、H.
(1)求证:CF=CH;
(2)如图(2),△ABC不动,将△EDC绕点C旋转到∠BCE= 时,试判断四边形AC
时,试判断四边形AC DM是什么四边形?并证明你的结论.
DM是什么四边形?并证明你的结论.
解:(1)证明:在△ACB和△ECD中
∵∠ACB=∠ECD=
∴∠1+∠ECB=∠2+∠ECB,
∴ ∠1=∠2………………………………………………………(2分)
又∵AC="CE=CB=CD, "
∴∠A=∠D= ………………………………………………(2分)
………………………………………………(2分)
∴△ACB≌△ECD, ∴CF="CH" ……………………………(2分)
(2)答: 四边形ACDM是菱形……………………………………………(1分)
证明: ∵∠ACB=∠ECD= , ∠BCE=
, ∠BCE=
∴∠1= , ∠2=
, ∠2=

又∵∠E=∠B= ,
,
∴∠1=∠E, ∠2=∠B…………………………………………(2分)
∴AC∥MD, CD∥AM ,
∴四边形ACDM是平行四边形…………………………… …(2分)
…(2分)
又∵AC="CD, " ∴四边形ACDM是菱形……………………(2分)
解析

练习册系列答案
相关题目
 沿y轴向下平移3个单位长度后恰好经过B(-3,0)及y轴上的C点.若抛物线
沿y轴向下平移3个单位长度后恰好经过B(-3,0)及y轴上的C点.若抛物线 与
与 轴交于A,B两点(点A在点B的右侧),且经过点C,(1)求直线
轴交于A,B两点(点A在点B的右侧),且经过点C,(1)求直线 及抛物线的解析式;(2)设抛物线的顶点为
及抛物线的解析式;(2)设抛物线的顶点为 ,点
,点 在抛物线的对称轴上,且
在抛物线的对称轴上,且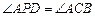 ,求点
,求点
 果DE2=BE·CE,求证四边形ABFC是矩形.
果DE2=BE·CE,求证四边形ABFC是矩形.



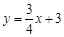 的图 像与y轴交于点A,点M在正比例函数
的图 像与y轴交于点A,点M在正比例函数 的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.