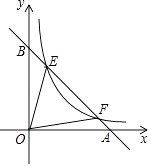题目内容
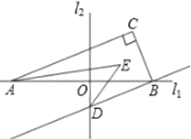
【题目】如图,直线![]() 直线
直线![]() ,垂足为
,垂足为![]() ,
,![]() 如图放置,过点
如图放置,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,在
,在![]() 内取一点
内取一点![]() ,连接
,连接![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,则
,则![]() _______.
_______.
(2)若![]() ,
,![]() ,则
,则![]() _______°.(用含
_______°.(用含![]() 的代数式表示)
的代数式表示)
【答案】40° ![]()
【解析】
(1)如图,过点E作EF//AC,交BC于F,根据平行线得性质可求出∠AEF和∠DEF的度数,利用周角得定义可得∠AED=∠CAE+∠EDB,即可求出∠AED的度数;
(2)由(1)可知∠AED=∠CAE+∠EDB,根据平行线的性质可得∠CAB=∠OBD,根据![]()
![]() 可得∠OBD+∠ODB=90°,根据
可得∠OBD+∠ODB=90°,根据![]() ,
,![]() 即可得答案.
即可得答案.
(1)如图,过点E作EF//AC,交BC于F,
∵BD//AC,
∴EF//AC//BD,
∴∠AEF=180°-∠CAE,∠DEF=180°-∠EDB,
∴∠AED=360°-∠AEF-∠DEF=∠CAE+∠EDB,
∵![]() ,
,![]() ,
,
∴∠AED=15°+25°=40°,
故答案为:40°

(2)∵AC//BD,
∴∠CAB=∠OBD,
∵![]()
![]() ,
,
∴∠OBD+∠ODB=90°,
∴∠CAB+∠ODB=90°,
由(1)得∠AED =∠CAE+∠EDB,
∵![]() ,
,![]() ,
,
∴∠AED=![]() ∠CAB+
∠CAB+![]() ∠ODB=
∠ODB=![]() (∠CAB+∠ODB)=
(∠CAB+∠ODB)=![]() ,
,
故答案为:![]()

练习册系列答案
相关题目