题目内容
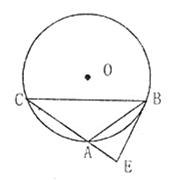
如图,△ABC内接于⊙O,过点B作⊙O的切线,交于CA的延长线于点E,∠EBC=2∠C.
(1)求证:AB=AC;(2)当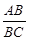 =
=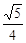 时,①求tan∠ABE的值;②如果AE=
时,①求tan∠ABE的值;②如果AE=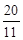 ,求AC的值。
,求AC的值。

(1)求证:AB=AC;(2)当
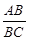 =
=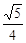 时,①求tan∠ABE的值;②如果AE=
时,①求tan∠ABE的值;②如果AE=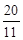 ,求AC的值。
,求AC的值。(1)证明见解析(2) ①1/2②4
(1)证明:∵BE切⊙O于点B,
∴∠ABE=∠C。························1分
∵∠EBC=2∠C,
即 ∠ABE+∠ABC=2∠C。
∴∠ABC=∠C。
∴AB=AC。····························2分
(2)解①如图,连接AO,交BC于点F。

∵AB=AC∴
∴AO⊥BC,且BF=FC。·······················3分
∵ ∴
∴ ∴
∴ …………………….….…….4分
…………………….….…….4分
设 ,
, ,
,
由勾股定理,得AF= =
= ………………5分
………………5分
∴ ……………………………6分
……………………………6分
②在 EBA和
EBA和 ECB中,
ECB中,
∵∠E=∠E, ∠EBA=∠ECB, ∴△EBA∽△ECB,
∴ =
=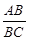 ……………………………7分
……………………………7分
∵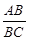 =
=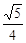
∴ (※)…………………8分
(※)…………………8分
由切割线定理,得
将(※)式代入上式,得 …………………………9分
…………………………9分
∵ ,
,
∴ ………………………………………………10分
………………………………………………10分
(1)BE切⊙O于点B,根据弦切角定理得到∠ABE=∠C,把求证AB=AC的问题转化为证明∠ABC=∠C的问题.
(2)①连接AO,交BC于点F,tan∠ABE=tan∠ABF= ,转化为求AF的问题.
,转化为求AF的问题.
②在△EBA和△ECB中,∠E=∠E,∠EBA=∠ECB,得到△EBA∽△ECB,再由切割线定理,得EB2=EA×EC=EA(EA+AC),就可以求出AC的长
∴∠ABE=∠C。························1分
∵∠EBC=2∠C,
即 ∠ABE+∠ABC=2∠C。
∴∠ABC=∠C。
∴AB=AC。····························2分
(2)解①如图,连接AO,交BC于点F。

∵AB=AC∴

∴AO⊥BC,且BF=FC。·······················3分
∵
 ∴
∴ ∴
∴ …………………….….…….4分
…………………….….…….4分设
 ,
, ,
,由勾股定理,得AF=
 =
= ………………5分
………………5分∴
 ……………………………6分
……………………………6分②在
 EBA和
EBA和 ECB中,
ECB中, ∵∠E=∠E, ∠EBA=∠ECB, ∴△EBA∽△ECB,
∴
 =
=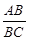 ……………………………7分
……………………………7分∵
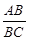 =
=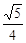
∴
 (※)…………………8分
(※)…………………8分由切割线定理,得

将(※)式代入上式,得
 …………………………9分
…………………………9分∵
 ,
,∴
 ………………………………………………10分
………………………………………………10分(1)BE切⊙O于点B,根据弦切角定理得到∠ABE=∠C,把求证AB=AC的问题转化为证明∠ABC=∠C的问题.
(2)①连接AO,交BC于点F,tan∠ABE=tan∠ABF=
 ,转化为求AF的问题.
,转化为求AF的问题.②在△EBA和△ECB中,∠E=∠E,∠EBA=∠ECB,得到△EBA∽△ECB,再由切割线定理,得EB2=EA×EC=EA(EA+AC),就可以求出AC的长

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
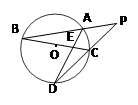

 .
.

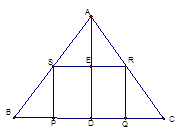
 ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,AB=AC.四边形PQRS是正方形。
ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,AB=AC.四边形PQRS是正方形。