题目内容
(2013年四川泸州4分)如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数 (x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),则点P3的坐标是 ;点Pn的坐标是 (用含n的式子表示).
(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),则点P3的坐标是 ;点Pn的坐标是 (用含n的式子表示).

【答案】
 ;
; 。
。
【解析】过点P1作P1E⊥x轴于点E,过点P2作P2F⊥x轴于点F,过点P3作P3G⊥x轴于点G,

∵△P1OA1是等腰直角三角形,∴P1E=OE=A1E=OA1。
设点P1的坐标为(a,a)(a>0),
将点P1(a,a)代入 ,可得a=1。
,可得a=1。
∴点P1的坐标为(1,1)。∴OA1=2a。
设点P2的坐标为(b+2,b),
将点P1(b+2,b)代入 ,可得b=
,可得b= ﹣1,
﹣1,
∴点P2的坐标为( +1,
+1, ﹣1)。∴A1F=A2F=2
﹣1)。∴A1F=A2F=2 ﹣2,OA2=OA1+A1A2=2
﹣2,OA2=OA1+A1A2=2 。
。
设点P3的坐标为(c+2 ,c),将点P1(c+2
,c),将点P1(c+2 ,c)代入y=,可得c=
,c)代入y=,可得c= ﹣
﹣ 。
。
∴点P3的坐标为
综上可得:P1的坐标为(1,1),P2的坐标为( +1,
+1, ﹣1),P3的坐标为
﹣1),P3的坐标为 b。
b。
总结规律可得:Pn坐标为: 。
。
考点:探索规律题(图形的变化类),反比例函数综合题,曲线上点的坐标与方程的关系,等腰直角三角形的性质。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
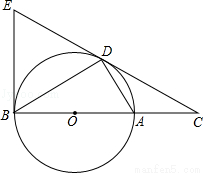
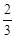 ,求BE的长.
,求BE的长.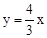 与反比例函数
与反比例函数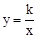 (x>0)的图象交于点A.将
(x>0)的图象交于点A.将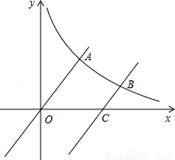
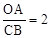 ,求反比例函数的解析式.
,求反比例函数的解析式.