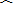题目内容
如图，BC是⊙O直径，点A为CB延长线上一点，AP切⊙O于点P，若AP=12，AB：BC=4：5，则⊙O的半径等于（ ）
| A．4 | B．5 | C．6 | D．7 |
连接OP，
∵AB：BC=4：5，
∴设AB=4x，则BC=5x，AC=9x，
∵AP切⊙O于点P，
∴AP2=AB•AC，
∴122=4x•9x，
解得：x=2，
则OA=AB+
BC=4x+
x=
x=
×2=13，
在直角△APO中，半径OP=
=
=5．
故选B．
∵AB：BC=4：5，
∴设AB=4x，则BC=5x，AC=9x，
∵AP切⊙O于点P，
∴AP2=AB•AC，
∴122=4x•9x，
解得：x=2，
则OA=AB+
| 1 |
| 2 |
| 5 |
| 2 |
| 13 |
| 2 |
| 13 |
| 2 |
在直角△APO中，半径OP=
| OA2-AP2 |
| 132-122 |
故选B．
练习册系列答案
相关题目
