题目内容
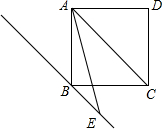 (2013•大兴区一模)已知:如图,过正方形ABCD的顶点B作直线BE平行于对角线AC,AE=AC(E,C均在AB的同侧).
(2013•大兴区一模)已知:如图,过正方形ABCD的顶点B作直线BE平行于对角线AC,AE=AC(E,C均在AB的同侧).求证:∠CAE=2∠BAE.
分析:先过A作AG⊥BE于G,连结BD交AC于点O,得出AGBO是正方形,AG=AO=
AC=
AE,再根据在直角三角形中,30°所对的直角边等于斜边的一半,求出∠AEG=30°,根据BE∥AC,求出∠CAE=∠AEG=30°,即可求出∠BAE的度数,从而证出∠CAE=2∠BAE.
| 1 |
| 2 |
| 1 |
| 2 |
解答: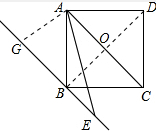 证明:过A作AG⊥BE于G,连结BD交AC于点O,
证明:过A作AG⊥BE于G,连结BD交AC于点O,
∵ABCD是正方形,
∴AGBO是正方形,
∴AG=AO=
AC=
AE,
∴∠AEG=30°,
∵BE∥AC,
∴∠CAE=∠AEG=30°.
∴∠BAE=45°-30°=15°.
∴∠CAE=2∠BAE.
 证明:过A作AG⊥BE于G,连结BD交AC于点O,
证明:过A作AG⊥BE于G,连结BD交AC于点O,∵ABCD是正方形,
∴AGBO是正方形,
∴AG=AO=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AEG=30°,
∵BE∥AC,
∴∠CAE=∠AEG=30°.
∴∠BAE=45°-30°=15°.
∴∠CAE=2∠BAE.
点评:此题考查了正方形的性质,解答本题要充分利用正方形的特殊性质,对角线互相垂直平分且相等,在直角三角形中,30°所对的直角边等于斜边的一半.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
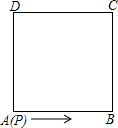 (2013•大兴区一模)如图,正方形ABCD边长为2cm,动点P从A点出发,沿正方形的边按逆时针方向运动,当它的运动路程为2013cm时,线段PA的长为
(2013•大兴区一模)如图,正方形ABCD边长为2cm,动点P从A点出发,沿正方形的边按逆时针方向运动,当它的运动路程为2013cm时,线段PA的长为