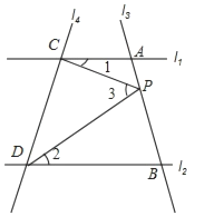
��Ŀ����
����Ŀ����ͼ��������״����С��ȫ��ͬ�ĺ���30����60����ֱ�����ǰ���ͼ�ٷ��ã�PA��PB��ֱ��MN�غϣ������ǰ�PAC�����ǰ�PBD�����Ƶ�P��ʱ����ת��
��1��ֱ��д����DPC�Ķ�����
��2����ͼ�ڣ���ͼ�ٻ����ϣ������ǰ�PAC�ı�PA��PN����ʼ�Ƶ�P��ʱ����ת��ת��Ϊ5��/�룬ͬʱ���ǰ�PBD�ı�PB��PM����ʼ�Ƶ�P��ʱ����ת��ת��Ϊ1��/�룬����PAת����PM�غ�ʱ�������ǰ嶼ֹͣת����������ת�����У���PC��PB�غ�ʱ������ת��ʱ���Ƕ��٣�
��3���ڣ�2���������£�PC��PB��PD���������У�������һ������ƽ�����������ߵļн�ʱ����ֱ��д����ת��ʱ�䣮

���𰸡���1��90������2����ת��ʱ����30��ʱPC��PB�غϣ���3��15���26.25���37.5��ʱ����һ������ƽ�����������ߵļнǣ�
��������
��1���á�DPC=180��-��APC-��BPD������
��2��ֻ������ת��ʱ����t��ʱPC��PB�غϣ��з��̽�ɵ�
��3��һ������ƽ�����������ߵļнǣ��������������PDƽ�֡�BPCʱ����PCƽ�֡�BPCʱ����PBƽ�֡�DPCʱ������ÿ�������Ӧ��ʱ�伴�ɣ�
�⣺
��1����DPC=180��-��APC-��BPD=180��-60��-30��=90��
�ʴ�Ϊ��90��
��2������ת��ʱ����t��ʱPC��PB�غϣ����������з��̵�
5t-t=30+90
���t=30
�֡�180��5=36��
��30��36
����ת��ʱ����30��ʱPC��PB�غϣ�
��3����t��ʱ����һ������ƽ�����������ߵļнǣ������������
�ٵ�PDƽ�֡�BPCʱ��5t-t=90-30�����t=15
�ڵ�PCƽ�֡�BPCʱ��![]() �����t=26.25
�����t=26.25
�۵�PBƽ�֡�DPCʱ��5t-t=90-2��30�����t=37.5
��15���26.25���37.5��ʱ����һ������ƽ�����������ߵļнǣ�

 ��У����ϵ�д�
��У����ϵ�д�