题目内容
学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3:2,求两种球各有多少个?若设篮球有x个,排球有y个,依题意,得到的方程组是( )
A. 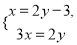 B.
B. 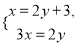 C.
C. 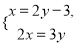 D.
D. 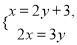
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
题目内容
学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3:2,求两种球各有多少个?若设篮球有x个,排球有y个,依题意,得到的方程组是( )
A. 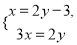 B.
B. 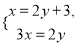 C.
C. 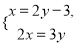 D.
D. 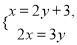
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案