题目内容
解方程、计算题
(1)x2-4x-5=0(配方法)
(2)4x2-4
x+5=0(公式法)
(3)(x-1)(x+2)=4
(4)计算:0.25•(cos60°)-2-(
-1)0+tan60°.
(1)x2-4x-5=0(配方法)
(2)4x2-4
| 5 |
(3)(x-1)(x+2)=4
(4)计算:0.25•(cos60°)-2-(
| 3 |
分析:(1)移项后配方得出(x-2)2=9,开方得到x-2=±3,求出方程的解即可;
(2)求出b2-4ac的值,代入公式x=
求出即可;
(3)整理后分解因式得出(x+3)(x-2)=0,推出x+3=0,x-2=0,求出方程的解即可;
(4)根据特殊角的三角函数值、零指数幂、负指数幂分别求出每一部分的值,再代入求出即可.
(2)求出b2-4ac的值,代入公式x=
-b±
| ||
| 2a |
(3)整理后分解因式得出(x+3)(x-2)=0,推出x+3=0,x-2=0,求出方程的解即可;
(4)根据特殊角的三角函数值、零指数幂、负指数幂分别求出每一部分的值,再代入求出即可.
解答:(1)解:移项得:x2-4x=5,
配方得:x2-4x+4=5+4,
即(x-2)2=9,
开方得:x-2=±3,
解得:x1=5,x2=-1;
(2)解:4x2-4
x+5=0,
∵b2-4ac=(4
)2-4×4×5=0,
∴x=
,
即x1=x2=
;
(3)解:(x-1)(x+2)=4
整理得:x2+x-6=0,
(x+3)(x-2)=0,
x+3=0,x-2=0,
解得:x1=-3,x2=2;
(4)解:原式=
×(
)-2-1+
=
×4-1+
=1-1+
=
.
配方得:x2-4x+4=5+4,
即(x-2)2=9,
开方得:x-2=±3,
解得:x1=5,x2=-1;
(2)解:4x2-4
| 5 |
∵b2-4ac=(4
| 5 |
∴x=
4
| ||||
| 2×4 |
即x1=x2=
| ||
| 2 |
(3)解:(x-1)(x+2)=4
整理得:x2+x-6=0,
(x+3)(x-2)=0,
x+3=0,x-2=0,
解得:x1=-3,x2=2;
(4)解:原式=
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
=
| 1 |
| 4 |
| 3 |
=1-1+
| 3 |
=
| 3 |
点评:本题考查了解一元二次方程、零指数幂、负指数幂、特殊角的三角函数值等知识点,解(1)(2)(3)的关键是把一元二次方程转化成解一元一次方程,解(4)关键是求出每一部分的值.

练习册系列答案
相关题目


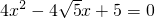 (公式法)
(公式法) -1)0+tan60°.
-1)0+tan60°. (公式法)
(公式法) -1)+tan60°.
-1)+tan60°.