题目内容
将矩形ABCD沿EF折叠，使点B与AD上的点B'重合，如BE=4，AB'=3，则BF的长为
- A.
- B.
- C.12
- D.15
B
分析：根据对称性可以得到B′E=BE=4，利用勾股定理即可求得AE的长度，然后证明：△ABB′∽△BFE，利用相似三角形的对应边的比相等即可求解．
解答：
解：∵B′E=BE=4，
∴直角△AEB′中，AE=
=
=
．
∴AB=BE+AE=4+，
∵直角△BEF中，BB′⊥EF，
∴∠ABB′=∠EFB
又∵∠A=∠ABF=90°，
∴△ABB′∽△BFE，
∴
=
即
=
，
解得：BF=．
点评：本题考查了翻折变换，以及相似三角形的判定与性质，正确证明△ABB′∽△BFE是关键．
分析：根据对称性可以得到B′E=BE=4，利用勾股定理即可求得AE的长度，然后证明：△ABB′∽△BFE，利用相似三角形的对应边的比相等即可求解．
解答：
解：∵B′E=BE=4，∴直角△AEB′中，AE=
==．∴AB=BE+AE=4+
，∵直角△BEF中，BB′⊥EF，
∴∠ABB′=∠EFB
又∵∠A=∠ABF=90°，
∴△ABB′∽△BFE，
∴
=即
=，解得：BF=
．点评：本题考查了翻折变换，以及相似三角形的判定与性质，正确证明△ABB′∽△BFE是关键．
练习册系列答案
相关题目
8、如图，在矩形ABCD中，AB=12cm，BC=6cm．点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A1、D1处，则整个阴影部分图形的周长为
（2012•内江）如图，在矩形ABCD中，AB=10，BC=5，点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A1、D1处，则阴影部分图形的周长为（ ）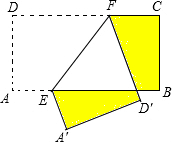
如图，在矩形ABCD中，AB=11cm，BC=6cm，点E、F分别在AB、CD上．将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A′、D′处，则整个阴影部分图形的周长为（ ）
（2013•相城区模拟）如图，将矩形ABCD沿EF折叠，C点落在C′处，D点落在D′处．若∠EFC=119°，则∠BFC′=
如图，将矩形ABCD沿EF折叠，使点D与点B重合，已知AB=3，AD=9，求BE的长．