题目内容
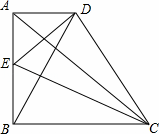
如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD.
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由.
考点:
直角梯形;全等三角形的判定与性质;线段垂直平分线的性质;等腰三角形的判定..
专题:
几何综合题;压轴题.
分析:
(1)把要证明的线段AD和BE放到两个三角形ABD和BCE中即可证明;
(2)根据等腰三角形的三线合一即可证明;
(3)根据(2)中的结论,即可证明CD=BC.
解答:
(1)证明:∵∠ABC=90°,BD⊥EC,
∴∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,
在△BAD和△CBE中,
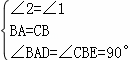 ,
,
∴△BAD≌△CBE(ASA),
∴AD=BE.
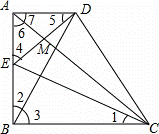
(2)证明:∵E是AB中点,
∴EB=EA,
∵AD=BE,
∴AE=AD,
∵AD∥BC,
∴∠7=∠ACB=45°,
∵∠6=45°,
∴∠6=∠7,
又∵AD=AE,
∴AM⊥DE,且EM=DM,
即AC是线段ED的垂直平分线;
(3)解:△DBC是等腰三角形(CD=BD).
理由如下:
∵由(2)得:CD=CE,由(1)得:CE=BD,
∴CD=BD.
∴△DBC是等腰三角形.
点评:
综合运用了全等三角形的性质和判定以及等腰三角形的性质.此类题注意已证明的结论的充分运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
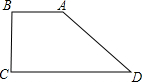 如图所示,在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AD=20,BC=10,则∠A和∠D分别是( )
如图所示,在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AD=20,BC=10,则∠A和∠D分别是( )| A、30°,150° | B、45°,135° | C、120°,60° | D、150°,30° |
 27、如图所示,在直角梯形ABCD中,AD∥BC,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边向B以3cm/s的速度运动.P,Q分别从A,C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t(s),t分别为何值时,四边形PQCD是平行四边形?等腰梯形?
27、如图所示,在直角梯形ABCD中,AD∥BC,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边向B以3cm/s的速度运动.P,Q分别从A,C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t(s),t分别为何值时,四边形PQCD是平行四边形?等腰梯形?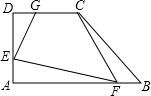 如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围.
如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围.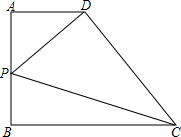 如图所示,在直角梯形ABCD中,AB=2,P是边AB的中点,∠PDC=90°,问梯形ABCD面积的最小值是多少?
如图所示,在直角梯形ABCD中,AB=2,P是边AB的中点,∠PDC=90°,问梯形ABCD面积的最小值是多少? (2013•山西模拟)如图所示,在直角梯形ABCD中,AB∥CD,点E为AB的中点,点F为BC的中点,AB=4,EF=2,∠B=60°,则AD的长为
(2013•山西模拟)如图所示,在直角梯形ABCD中,AB∥CD,点E为AB的中点,点F为BC的中点,AB=4,EF=2,∠B=60°,则AD的长为