题目内容
 如图,已知△ABC是一等腰三角形铁板余料,其中AB=AC=20cm,BC=24cm.若在△ABC上截出一矩形零件DEFG,使EF在BC上,点D、G分别在边AB、AC上.问矩形DEFG的最大面积是多少?
如图,已知△ABC是一等腰三角形铁板余料,其中AB=AC=20cm,BC=24cm.若在△ABC上截出一矩形零件DEFG,使EF在BC上,点D、G分别在边AB、AC上.问矩形DEFG的最大面积是多少?
分析:矩形面积为长×宽,可以先设出未知数DE=x,再把另一边用x表示出来,求出面积表达式,再根据x的取值范围求取最大值.
解答: 解:过A作AM⊥BC于M,交DG于N,
解:过A作AM⊥BC于M,交DG于N,
∵△ABC是等腰三角形,AM⊥BC,
∴BM=CM=
BC(三线合一),
则AM=
=16(cm).
设DE=xcm,S矩形=ycm2,
∵四边形DGFE是矩形,
∴DG∥BC,
∴△ADG∽△ABC,
故
=
,即
=
,
故DG=
(16-x).
∴y=DG•DE=
(16-x)x=-
(x2-16x)=-
(x-8)2+96,
从而当x=8时,y有最大值96.
答:矩形DEFG的最大面积是96cm2.
 解:过A作AM⊥BC于M,交DG于N,
解:过A作AM⊥BC于M,交DG于N,∵△ABC是等腰三角形,AM⊥BC,
∴BM=CM=
| 1 |
| 2 |
则AM=
| 202-122 |
设DE=xcm,S矩形=ycm2,
∵四边形DGFE是矩形,
∴DG∥BC,
∴△ADG∽△ABC,
故
| AN |
| AM |
| DG |
| BC |
| 16-x |
| 16 |
| DG |
| 24 |
故DG=
| 3 |
| 2 |
∴y=DG•DE=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
从而当x=8时,y有最大值96.
答:矩形DEFG的最大面积是96cm2.
点评:本题本质是考查二次函数的应用,以及二次函数求最值的问题,只要能熟练掌握,便能很容易的解决问题.

练习册系列答案
相关题目
 的坐标为(-1,0).
的坐标为(-1,0). 如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.
如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.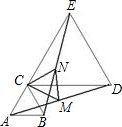 如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,
如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点, (2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF. (2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.
(2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.