题目内容
【题目】用正方形硬纸板做三棱柱盒子,如图1,每个盒子由 ![]() 个长方形侧面和
个长方形侧面和 ![]() 个三边均相等的三角形底面组成,硬纸板以如图2两种方法裁剪(裁剪后边角料不再利用),现有
个三边均相等的三角形底面组成,硬纸板以如图2两种方法裁剪(裁剪后边角料不再利用),现有 ![]() 张硬纸板,裁剪时
张硬纸板,裁剪时 ![]() 张用了
张用了 ![]() 方法,其余用
方法,其余用 ![]() 方法.
方法.
(1)求裁剪出的侧面和底面的个数(分别用含 ![]()
的代数式表示);
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
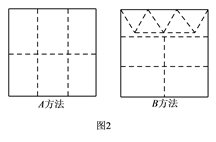
【答案】
(1)解: ![]() 裁剪时
裁剪时 ![]() 张用了
张用了 ![]() 方法,
方法,
![]() 裁剪时
裁剪时 ![]() 张用了
张用了 ![]() 方法
方法 ![]() 侧面的个数为:
侧面的个数为: ![]()
个,底面的个数为: ![]() 个
个
(2)解:由题意,得 ![]() ,
,
解得: ![]() ,则盒子的个数为:
,则盒子的个数为: ![]()
答:裁剪出的侧面和底面恰好全部用完,能做 ![]() 个盒子
个盒子
【解析】(1)根据题意得到裁剪时 ( 19 x ) 张用了B方法 , 侧面的个数为 6 x + 4 ( 19 x ),底面的个数为 5 ( 19 x);(2)根据题意得到3 ( 95 5 x ) = 2 ( 2 x + 76 ) ,求出能做的盒子数.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目