Question

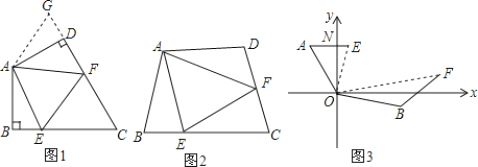
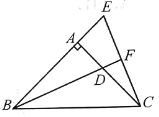
【题目】如图，在△ABC中，∠BAC=90°,AB=AC,D在AC上，E在BA的延长线上，BD=CE,BD的延长线交CE于点F。求证：BF⊥CE。

Answer 1

【答案】见解析

【解析】

由∠BAC=90°可得出∠CAE=90°，根据AB=AC、BD=CE可证出Rt△BAD≌Rt△CAE（HL），根据全等三角形的性质可得出∠E=∠ADB，进而可得出∠CDF=∠E，再根据∠E+∠ACE=90°结合三角形内角和定理可得出∠CFD=90°，即BF⊥CE．

证明：∵∠BAC=90°，
∴∠CAE=90°．
在Rt△BAD和Rt△CAE中，

，
∴Rt△BAD≌Rt△CAE（HL），
∴∠E=∠ADB．
∵∠ADB=∠CDF，
∴∠CDF=∠E．
∵∠E+∠ACE=90°，
∴∠CDF+∠DCF=90°，
∴∠CFD=90°，即BF⊥CE．