题目内容
(2003•随州)如图,已知直线y=x+b与双曲线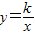 在第一象限内交于A点,交x轴于B点(B在O点左边).AC⊥x轴于C,且点C的坐标是(b,0).若△ABC的面积为8,求直线与双曲线的另一个交点坐标.
在第一象限内交于A点,交x轴于B点(B在O点左边).AC⊥x轴于C,且点C的坐标是(b,0).若△ABC的面积为8,求直线与双曲线的另一个交点坐标.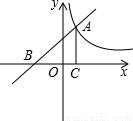
【答案】分析:应用b表示出A,B的坐标,利用△ABC的面积为8求得b的值,进而求得A,B坐标,把A代入反比例函数解析式就能求得解析式,把A,B代入一次函数解析式就能求得一次函数解析式,两个函数解析式组成方程组就能求得交点坐标.
解答:解:由y=x+b,
令y=0,得x=-b,
∴B(-b,0),
令x=b,得y=2b,
∴A(b,2b),
∵S△ABC=8,
∴ ×2b×2b=8,
×2b×2b=8,
解得b=2,(负值舍去),
又∵A在反比例函数解析式上,
∴k=2b2=8,
那么 ,
,
解得x=-4,y=-2,或x=2,y=4,
∵另一交点在第三象限,
∴坐标为(-4,-2).
点评:解决本题的关键是用b表示相关各点的坐标,利用三角形的面积求得在函数解析式上的各点.
解答:解:由y=x+b,
令y=0,得x=-b,
∴B(-b,0),
令x=b,得y=2b,
∴A(b,2b),
∵S△ABC=8,
∴
 ×2b×2b=8,
×2b×2b=8,解得b=2,(负值舍去),
又∵A在反比例函数解析式上,
∴k=2b2=8,
那么
 ,
,解得x=-4,y=-2,或x=2,y=4,
∵另一交点在第三象限,
∴坐标为(-4,-2).
点评:解决本题的关键是用b表示相关各点的坐标,利用三角形的面积求得在函数解析式上的各点.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
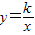 在第一象限内交于A点,交x轴于B点(B在O点左边).AC⊥x轴于C,且点C的坐标是(b,0).若△ABC的面积为8,求直线与双曲线的另一个交点坐标.
在第一象限内交于A点,交x轴于B点(B在O点左边).AC⊥x轴于C,且点C的坐标是(b,0).若△ABC的面积为8,求直线与双曲线的另一个交点坐标.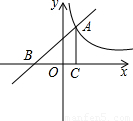
 -4π
-4π -
- π
π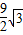 -4π
-4π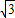 -
- π
π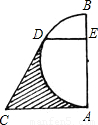
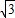 -4π
-4π -
- π
π -4π
-4π -
- π
π