题目内容
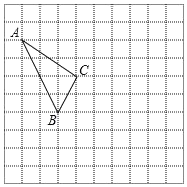
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是
是![]() 边上的动点.将
边上的动点.将![]() 沿AE折叠,点
沿AE折叠,点![]() 落在点
落在点![]() 处;将
处;将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处.当
处.当![]() 的长度为__________时,点
的长度为__________时,点![]() 与点
与点![]() 能重合.
能重合.

【答案】![]()
【解析】
由折叠的性质可得:∠AME=∠B=90°,∠FNE=∠C=90°,∠AEF=![]() ∠BEC=90°,BE=ME,CE=NE,若点
∠BEC=90°,BE=ME,CE=NE,若点![]() 与点
与点![]() 重合,则A、M、F三点共线,进而可得BE=CE
重合,则A、M、F三点共线,进而可得BE=CE![]() ,设DF=CF=x,利用勾股定理分别表示出AE2、EF2、AF2,由此可得关于x的方程,解方程即可求出x,进一步即得结果.
,设DF=CF=x,利用勾股定理分别表示出AE2、EF2、AF2,由此可得关于x的方程,解方程即可求出x,进一步即得结果.
解:由折叠的性质可得:∠AME=∠B=90°,∠FNE=∠C=90°,∠AEM=∠AEB,∠NEF=∠CEF,BE=ME,CE=NE,
若点![]() 与点
与点![]() 重合,则A、M、F三点共线,则BE= ME=NE=CE,∠AEF=
重合,则A、M、F三点共线,则BE= ME=NE=CE,∠AEF=![]() ∠BEC=90°,
∠BEC=90°,
∵![]() ,
,
∴BE=CE=2,
由于点![]() 是
是![]() 边的中点,可设DF=CF=x,则AB=CD=2x,
边的中点,可设DF=CF=x,则AB=CD=2x,
在Rt△AEF中,由勾股定理,得:![]() ,
,
即![]() ,解得:
,解得:![]() ,
,
∴![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目