题目内容
在等腰△ABC中，∠A=30°，AB=8，则AB边上的高CD的长是 ．
4或
或
。
或。根据题意画出AB=AC，AB=BC和AC=BC时的图象，然后根据等腰三角形的性质和解直角三角形，分别进行计算即可：
(1)如图，
当AB=AC时，
∵∠A=30°，
∴CD=
AC=×8=4。
（2）如图，当AB=BC时，
则∠A=∠ACB=30°。
∴∠ACD=60°。∴∠BCD=30°
∴CD=cos∠BCD•BC=cos30°×8=4。
（3）如图，当AC=BC时，
则AD=4。
∴CD=tan∠A•AD=tan30°•4=。
综上所述，AB边上的高CD的长是4或或。
(1)如图，
当AB=AC时，
∵∠A=30°，
∴CD=
AC=×8=4。（2）如图，当AB=BC时，
则∠A=∠ACB=30°。
∴∠ACD=60°。∴∠BCD=30°
∴CD=cos∠BCD•BC=cos30°×8=4
。（3）如图，当AC=BC时，
则AD=4。
∴CD=tan∠A•AD=tan30°•4=
。综上所述，AB边上的高CD的长是4或
或。
练习册系列答案
相关题目
中，
，
，分别以
，
为直径作半圆，面积分别记为
，
，则
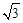≈1.732，结果保留三个有效数字）．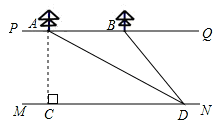
，
，
，
）。
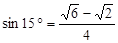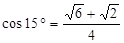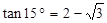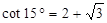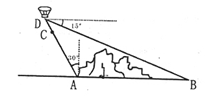
，BC=
，则sinB= .