题目内容
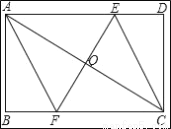
如图，在矩形ABCD中，E，F分别为边AD，BC上的点，AE=CF，对角线AC平分∠ECF．
（1）求证：四边形AECF为菱形．
（2）已知AB=4，BC=8，求菱形AECF的面积．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
周周清检测系列答案轻巧夺冠周测月考直通高考系列答案题目内容
如图，在矩形ABCD中，E，F分别为边AD，BC上的点，AE=CF，对角线AC平分∠ECF．
（1）求证：四边形AECF为菱形．
（2）已知AB=4，BC=8，求菱形AECF的面积．
周周清检测系列答案轻巧夺冠周测月考直通高考系列答案
如图
，已知抛物线
，经过点
、
．
求此抛物线顶点C的坐标；
联结AC交y轴于点D，联结BD、BC，过点C作
，垂足为点H，抛物线对称轴交x轴于G，联结HG，求HG的长．
，以后该车的年折旧率有所变化，但它在第二、三年的年折旧率相同
已知在第三年年末，这辆车折旧后价值
万元，求这辆车第二、三年的年折旧率．
有一根为0，则m的值为
C. 2 D. 
，则放入口袋中的黄球个数是_____．