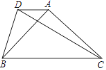
题目内容
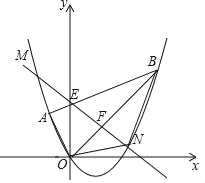
【题目】如图,正方形![]() 的边长为2,点
的边长为2,点![]() 为坐标原点,边
为坐标原点,边![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,点
轴上,点![]() 是
是![]() 的中点.点
的中点.点![]() 是线段
是线段![]() 上的一个点,如果将
上的一个点,如果将![]() 沿直线
沿直线![]() 对折,使点
对折,使点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 所在直线上.
所在直线上.
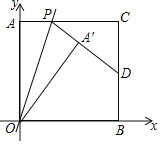
(1)若点![]() 是端点,即当点
是端点,即当点![]() 在
在![]() 点时,
点时,![]() 点的位置关系是________,
点的位置关系是________,![]() 所在的直线是__________;当点
所在的直线是__________;当点![]() 在
在![]() 点时,
点时,![]() 点的位置关系是________,
点的位置关系是________,![]() 所在的直线表达式是_________;
所在的直线表达式是_________;
(2)若点![]() 不是端点,用你所学的数学知识求出
不是端点,用你所学的数学知识求出![]() 所在直线的表达式;
所在直线的表达式;
(3)在(2)的情况下,![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的周长为最小值?若存在,请求出点
的周长为最小值?若存在,请求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
【答案】(1)A,y轴;B,y=x;(2)y=3x;(3)存在.由于,理由见解析.
【解析】
(1)由轴对称的性质可得出结论;
(2)连接OD,求出OD=![]() ,设点P(
,设点P(![]() ,2),PA′=
,2),PA′=![]() ,PC=
,PC=![]() ,CD=1.可得出(
,CD=1.可得出(![]() )2=(2
)2=(2![]() )2+12,解方程可得解x=
)2+12,解方程可得解x=![]() .求出P点的坐标即可得出答案;
.求出P点的坐标即可得出答案;
(3)可得出点D关于![]() 轴的对称点是D′(2,-1),求出直线PD′的函数表达式为
轴的对称点是D′(2,-1),求出直线PD′的函数表达式为![]() ,则答案可求出.
,则答案可求出.
(1)由轴对称的性质可得,若点P是端点,即当点P在A点时,A′点的位置关系是点A,
OP所在的直线是y轴;
当点P在C点时,
∵∠AOC=∠BOC=45°,
∴A′点的位置关系是点B,
OP所在的直线表达式是y=x.
故答案为:A,y轴;B,y=x;
(2)连接OD,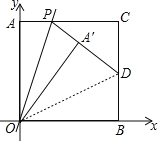
∵正方形AOBC的边长为2,点D是BC的中点,
∴OD=![]() .
.
由折叠的性质可知,OA′=OA=2,∠OA′D=90°.
∵OA′=OA= OB=2,OD公共,
∴![]() (
(![]() ),
),
∴A′D=BD=1.
设点P(![]() ,2),则PA′=
,2),则PA′=![]() ,PC=
,PC=![]() ,CD=1,
,CD=1,
∴![]() ,即(
,即(![]() )2=(
)2=(![]() )2+12,
)2+12,
解得:![]() .
.
所以P(![]() ,2),
,2),
设OP所在直线的表达式为![]() ,
,
将P(![]() ,2)代入得:
,2)代入得:![]() ,
,
解得:![]() ,
,
∴OP所在直线的表达式是![]() ;
;
(3)存在.
若△DPQ的周长为最小,
即是要PQ+DQ为最小,
作点D关于x轴的对称点是D′,
连接D′P交x轴于点Q,此时使![]() 的周长取得最小值,
的周长取得最小值,
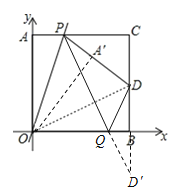
∵点D关于x轴的对称点是D′(2,![]() ),
),
∴设直线PD'的解析式为![]() ,
,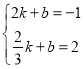 ,
,
解得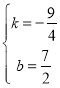 ,
,
∴直线PD′的函数表达式为![]() .
.
当![]() 时,
时,![]() .
.
∴点Q的坐标为:(![]() ,0).
,0).