题目内容
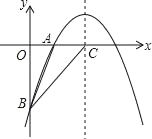
如图,二次函数y=﹣ x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
题目内容
如图,二次函数y=﹣ x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案