题目内容
如图1,在△ABC中,E、D分别为AB、AC上的点,且ED//BC,O为DC中点,连结EO并延长交BC的延长线于点F,则有S四边形EBCD=S△EBF.
(1)如图2,在已知锐角∠AOB内有一个定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.将直线MN绕着点P旋转的过程中发现,当直线MN满足某个条件时,△MON的面积存在最小值.直接写出这个条件:_______________________.
(2)如图3,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)、(6,3)、( ,
, )、(4、2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.
)、(4、2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.

解:(1)当直线MN旋转到点P是线段MN的中点时, △MON的面积最小.
(2)分两种情况:
①如图3①过点P的直线l 与四边形OABC 的一组对边 OC、AB分别交于点M、N.
延长OC、AB交于点D,易知AD = 6,S△OAD=18 .
由(1)的结论知,当PM=PN时,△MND的面积最小,此时四边形OANM的面积最大.
过点P、M分别作PP1⊥OA,MM1⊥OA,垂足分别为P1、M1.
由题意得M1P1=P1A = 2,从而OM1=MM1= 2. 又P(4,2),B(6,3)
∴P1A=M1P1=O M1=P1P=2,M1 M=OM=2,可证四边形MM1P1P是正方形.
∴MN∥OA,∠MND=90°,NM=4,DN=4.求得S△MND=8 -
∴
 |
② 如图3②,过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N.
延长CB交x轴于T点,由B、C的坐标可得直线BC对应的函数关系式为 y =-x+9 .
则T点的坐标为(9,0).
∴S△OCT= 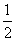 ×9×
×9× =
= .
.
由(1)的结论知:当PM=PN时,△MNT的面积最小,此时四边形OCMN的面积最大.
过点P、M点分别作PP1⊥OA,MM1⊥OA,垂足为P1 ,M1.
从而 NP1 =P1M1,MM1=2PP1=4.
∴点M的横坐标为5,点P(4、2),P1M1= NP1 = 1,TN =6.
∴S△MNT= 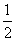 ×6×4=12,S四边形OCMN=S△OCT-S△MNT =
×6×4=12,S四边形OCMN=S△OCT-S△MNT =  -12=
-12= <10.
<10.
综上所述:截得四边形面积的最大值为10.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
 的抛物线的解析式,y= .
的抛物线的解析式,y= . D.
D.
 的值为零,则
的值为零,则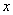 的值为 .
的值为 . 的绝对值是
的绝对值是 B. 3 C.
B. 3 C. 
 与反比例函数
与反比例函数 的图象交于A(1,4),B(-2,
的图象交于A(1,4),B(-2, )两点,
)两点, 图象直接写出不等式
图象直接写出不等式 的解集.
的解集.