题目内容
如图,点B、C、D都在⊙ O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2
O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2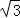 .
.
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
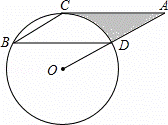
(1)证明:连接OC,交BD于E,
∵∠B=30°,∠B= ∠COD,
∠COD,
∴∠COD=60°,
∵∠A=30°,
∴∠OCA=90°,
即OC⊥AC,
∴AC是⊙O的切线;
(2)解:∵AC∥BD,∠OCA=90°,
∴∠OED=∠OCA=90°,
∴DE= BD=
BD=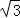 ,
,
∵sin∠COD= ,
,
∴OD=2,
在Rt△ACO中,tan∠COA= ,
,
∴AC=2 ,
,
∴S阴影= ×2×2
×2×2 ﹣
﹣ =2
=2 ﹣
﹣ .
.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
计算sin245°+cos30°•tan60°,其结果是( )
|
| A. | 2 | B. | 1 | C. |
| D. |
|
已知点A的坐标为(2,0),点P在直线y=x上运动,当以点P为圆心,PA的长为半径的圆的面积最小时,点P的坐标为( )
|
| A. | (1,﹣1) | B. | (0,0) | C. | (1,1) | D. | ( |





 ,
,