题目内容
已知：在直角三角形ABC中且∠B=90°，AD、CE分别是BC、AB边中线，AD=
，CE=
，求AC的长．
| 61 |
| 19 |
分析：先设AE=BE=x，CD=BD=y，再根据勾股定理得到关于x、y的方程组，分别求出x、y的值，再根据勾股定理即可得出AB的值．
解答：解：设AE=BE=x，CD=BD=y，
∵△ABD与△BCE是直角三角形，
∴
，
∴
解得：
，
∴AB=2
，BC=2，
∵∠B=90°，
∴AC=
=8．
∵△ABD与△BCE是直角三角形，
∴
|
∴
|
解得：
|
∴AB=2
| 15 |
∵∠B=90°，
∴AC=
| AB2 +BC2 |
点评：本题考查的是勾股定理，解答此类问题的关键是分别设出AE、BE、CD、BD的长，再根据勾股定理建立关于x、y的方程组．
练习册系列答案
考前必练系列答案
相关题目
已知：在直角三角形ABC中，两条直角边AC=6，BC=8．则角A的正弦值是（ ）
A、sinA=
| ||
B、sinA=
| ||
C、sinA=
| ||
D、sinA=
|
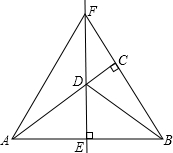已知：在直角三角形ABC中，∠ACB=90°，AC=4，BC=3，AB的垂直平分线交AB于E，AC于D，交BC的延长线于F．
已知：在直角三角形ABC中，∠ACB=90°，AC=4，BC=3，AB的垂直平分线交AB于E，AC于D，交BC的延长线于F．