题目内容
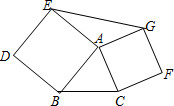 如图,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连接EG,则△ABC与△AEG的面积之间的关系为
如图,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连接EG,则△ABC与△AEG的面积之间的关系为
- A.S△ABC≥S△AEG
- B.S△ABC≤S△AEG
- C.S△ABC=S△AEG
- D.无法确定
C
分析:过点C作CM⊥AB于M,过点G作GN⊥EA交EA延长线于N,则∠AMC=∠ANG=90°,根据正方形性质得出∠BAE=∠CAG=90°,AB=AE,AC=AG,求出∠NAG=∠MAC,证△ACM≌△AGN(,推出CM=GN,根据三角形的面积公式求出即可.
解答:△ABC与△AEG面积相等,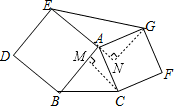 理由是:
理由是:
过点C作CM⊥AB于M,过点G作GN⊥EA交EA延长线于N,则∠AMC=∠ANG=90°,
∵四边形ABDE和四边形ACFG都是正方形,
∴∠BAE=∠CAG=90°,AB=AE,AC=AG,
∵∠BAE+∠CAG+∠BAC+∠EAG=360°,
∴∠BAC+∠EAG=180°,
∵∠EAG+∠GAN=180°,
∴∠BAC=∠GAN,
在△ACM和△AGN中,
 ,
,
∴△ACM≌△AGN(AAS),
∴CM=GN,
∵S△ABC= AB•CM,S△AEG=
AB•CM,S△AEG= AE•GN,
AE•GN,
∴S△ABC=S△AEG.
故选C.
点评:本题考查了正方形的性质,全等三角形的性质和判定,三角形的面积等知识点的应用,关键是作辅助线后求出CM=GN.
分析:过点C作CM⊥AB于M,过点G作GN⊥EA交EA延长线于N,则∠AMC=∠ANG=90°,根据正方形性质得出∠BAE=∠CAG=90°,AB=AE,AC=AG,求出∠NAG=∠MAC,证△ACM≌△AGN(,推出CM=GN,根据三角形的面积公式求出即可.
解答:△ABC与△AEG面积相等,
 理由是:
理由是:过点C作CM⊥AB于M,过点G作GN⊥EA交EA延长线于N,则∠AMC=∠ANG=90°,
∵四边形ABDE和四边形ACFG都是正方形,
∴∠BAE=∠CAG=90°,AB=AE,AC=AG,
∵∠BAE+∠CAG+∠BAC+∠EAG=360°,
∴∠BAC+∠EAG=180°,
∵∠EAG+∠GAN=180°,
∴∠BAC=∠GAN,
在△ACM和△AGN中,
 ,
,∴△ACM≌△AGN(AAS),
∴CM=GN,
∵S△ABC=
 AB•CM,S△AEG=
AB•CM,S△AEG= AE•GN,
AE•GN,∴S△ABC=S△AEG.
故选C.
点评:本题考查了正方形的性质,全等三角形的性质和判定,三角形的面积等知识点的应用,关键是作辅助线后求出CM=GN.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.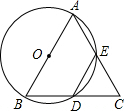 如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
 (2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E.
(2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E. (2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.
(2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.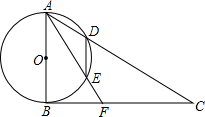 如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF
如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF