题目内容
已知,半径分别为1cm和2cm的⊙O1与⊙O2外切,则两圆的圆心距是
3
3
cm.分析:由半径分别为1cm和2cm的⊙O1与⊙O2外切,根据圆与圆的位置关系,即可得两圆的圆心距:d=R+r,即可求得答案.
解答:解:∵半径分别为1cm和2cm的⊙O1与⊙O2外切,
∴两圆的圆心距d=1+2=3(cm).
故答案为:3.
∴两圆的圆心距d=1+2=3(cm).
故答案为:3.
点评:此题考查了圆与圆的位置关系.此题比较简单,解题的关键是掌握两圆位置关系与数量关系间的联系:
外离,则P>R+r;外切,则P=R+r;相交,则R-r<P<R+r;内切,则P=R-r;内含,则P<R-r.(P表示圆心距,R,r分别表示两圆的半径).
外离,则P>R+r;外切,则P=R+r;相交,则R-r<P<R+r;内切,则P=R-r;内含,则P<R-r.(P表示圆心距,R,r分别表示两圆的半径).

练习册系列答案
相关题目
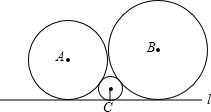
如图,已知圆心为A,B,C的三个圆彼此相切,且均与直线l相切.若⊙A,⊙B,⊙C的半径分别为a,b,c(0<c<a<b),则a,b,c一定满足的关系式为( )

| A、2b=a+c | ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|