题目内容

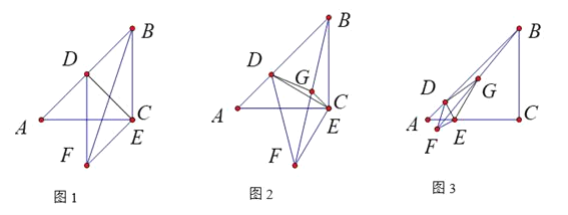
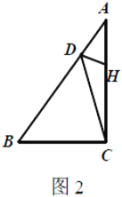
【题目】如图，把矩形沿对折，使与重合，折痕交于，连，若，，为上一个动点，则的最小值为________

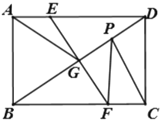
【答案】10

【解析】

先根据折叠的性质、三角形全等的判定定理与性质可得，，从而可得点E与点F关于BD对称，再根据两点之间线段最短得出的最小值为CE的长，过点A作于点H，根据平行线的性质、正切三角函数可得，从而设，再根据平行线分线段成比例定理分别可求出AE的长，然后利用正切三角函数值可求出AB的长，从而可得CD的长，由此即可得出答案．

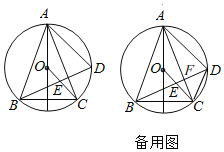
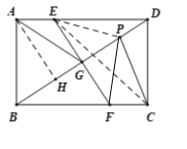
如图，连接PE、CE，过点A作于点H

由折叠的性质可知，

四边形ABCD是矩形

在和中，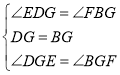

，

点E与点F关于BD对称，即BD垂直平分EF

由两点之间线段最短可知，当三点共线时，取得最小值，最小值为CE

，即

在中，

设，则

点G是矩形ABCD对角线的交点

，

，即

解得

在中，

在中，

解得

在中，

则的最小值为10

故答案为：10．

练习册系列答案
相关题目

【题目】如图，在等腰Rt△ABC中，∠ACB＝90°，AB＝．点D，E分别在边AB，AC上，将线段ED绕点E按逆时针方向旋转90°得到EF，连结BF，BF的中点为G．

（1）当点E与点C重合时．

①如图1，若AD＝BD，求BF的长．

②当点D从点A运动到点B时，求点G的运动路径长．

（2）当AE＝3，点G在△DEF一边所在直线上时，求AD的长．

【题目】如图，在锐角等腰三角形ABC中，AB＝AC，点O为△ABC外接圆的圆心，连结OC，过点B作AC的垂线，交⊙O于点D，交OC于点E，交AC于点F，连结AD和CD．

（1）若∠BAC＝2α，则∠BDA＝　 　（用含α的代数式表示）．

（2）①求证：OC∥AD；

②若E为OC的中点，求的值．

（3）若x＝，y＝，求y关于x的函数关系式．

【题目】在篮球比赛中，东东投出的球在点A处反弹，反弹后球运动的路线为抛物线的一部分（如图1所示建立直角坐标系），抛物线顶点为点B．

（1）求该抛物线的函数表达式．

（2）当球运动到点C时被东东抢到，CD⊥x轴于点D，CD＝2.6m．

①求OD的长．

②东东抢到球后，因遭对方防守无法投篮，他在点D处垂直起跳传球，想将球沿直线快速传给队友华华，目标为华华的接球点E（4，1.3）．东东起跳后所持球离地面高度h1（m）（传球前）与东东起跳后时间t（s）满足函数关系式h1＝﹣2（t﹣0.5）2+2.7（0≤t≤1）；小戴在点F（1.5，0）处拦截，他比东东晚0.3s垂直起跳，其拦截高度h2（m）与东东起跳后时间t（s）的函数关系如图2所示（其中两条抛物线的形状相同）．东东的直线传球能否越过小戴的拦截传到点E？若能，东东应在起跳后什么时间范围内传球？若不能，请说明理由（直线传球过程中球运动时间忽略不计）．

【题目】如图，⊙O是△ABC的外接圆，AB是直径，D是AC中点，直线OD与⊙O相交于E，F两点，P是⊙O外一点，P在直线OD上，连接PA，PC，AF，且满足∠PCA=∠ABC．

（1）求证：PA是⊙O的切线；

（2）证明：；

（3）若BC=8，tan∠AFP=，求DE的长．

【题目】（1）如图1，为上一点，若，，求证：．

（2）如图2，中，，为上一点，为上一点，，，，求．

（3）如图，在四边形中，，，，，直接写出的长．

【题目】如图，在中，、是对角线上两点，，，，则的大小为___________

【题目】疫情防控期间，学校开学初购进A、B两种消毒液，购买A种消毒液花费2500元，购买B种消毒液花费2000元，且A种消毒液数量是B种消毒液数量的2倍，一桶B种消毒液比一桶A种消毒液贵30元．

（1）求购买一桶A种、一桶B种消毒液各需多少元？

（2）为了加强防控，学校准备再次购买A、B两种消毒液共50桶，A种消毒液售价比第一次提高了8%，B种消毒液按第一次售价的9折出售，如果此次购买总费用不超过3260元，那么学校此次最多可购买多少桶B种消毒液？

【题目】阅读下面内容：我们已经学习了《二次根式》和《乘法公式》，聪明的你可以发现：当，时，∵，∴，当且仅当时取等号．请利用上述结论解决以下问题：

(1)当时，的最小值为_______；当时，的最大值为__________．

(2)当时，求的最小值．

(3)如图，四边形ABCD的对角线AC ，BD相交于点O，△AOB、△COD的面积分别为4和9，求四边形ABCD面积的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网