Question

【题目】如图，菱形ABCD，∠A=60°，AB=4，以点B为圆心的扇形与边CD相切于点E，扇形的圆心角为60°，点E是CD的中点，图中两块阴影部分的面积分别为S1 ， S2 ， 则S2﹣S1= ．

Answer 1

【答案】2 ﹣π
【解析】解：连接BE， ∵以点B为圆心的扇形与边CD相切于点E，
∵在菱形ABCD中，∠A=60°，AB=4，
∴BE⊥CD，
∵点E是CD的中点，
∴CE= CD=2，BE=2 ，∠EBC=30°，
∵扇形的圆心角为60°，
∴S2﹣S1= ×CEBE﹣ = 2×2 ﹣π=2 ﹣π．
所以答案是：2 ﹣π．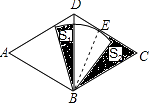

【考点精析】本题主要考查了菱形的性质和切线的性质定理的相关知识点，需要掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．